Introducción al Cálculo del Área de un Círculo
¡Hola! Soy Leandro y hoy vamos a explorar un tema fascinante: cómo calcular el área de un círculo mediante simulaciones. Si alguna vez te has preguntado cómo se puede aplicar la tecnología y las matemáticas para resolver problemas geométricos de manera precisa y eficiente, ¡has llegado al lugar correcto!
En este artículo, desglosaré mi experiencia y conocimientos sobre el tema, explicando en detalle cómo funcionan estas simulaciones, y cómo puedes utilizarlas tú mismo para obtener resultados sorprendentes. Además, te proporcionaré enlaces a recursos adicionales para que puedas profundizar en este interesante campo.
¿Qué es el Área de un Círculo?
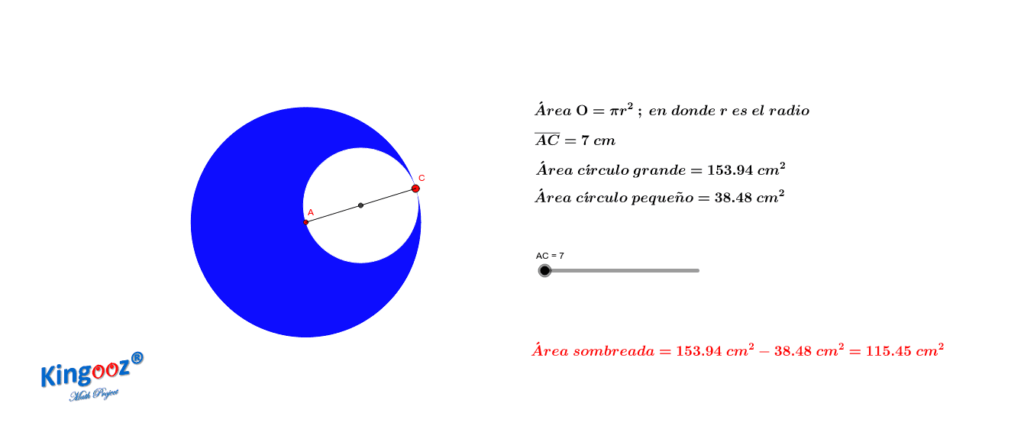
Antes de adentrarnos en las simulaciones, es importante entender qué es el área de un círculo. El área de un círculo es la cantidad de espacio que ocupa su superficie. Matemáticamente, se puede calcular utilizando la fórmula:
Área = π × r2
donde r es el radio del círculo y π (pi) es una constante matemática aproximadamente igual a 3.14159.
La Magia de las Simulaciones: ¿Qué son y para qué Sirven?
Las simulaciones son herramientas poderosas que nos permiten modelar situaciones del mundo real a través de programas de computadora. En el contexto del cálculo del área de un círculo, las simulaciones nos permiten aproximar esta área sin necesidad de realizar cálculos directos con fórmulas matemáticas. En su lugar, podemos utilizar métodos probabilísticos y estadísticos para obtener una estimación precisa.
El Método de Monte Carlo: Una Introducción
Uno de los métodos más populares para calcular el área de un círculo mediante simulaciones es el Método de Monte Carlo. Este método utiliza la generación de números aleatorios para aproximar el área de una figura geométrica. A continuación, te explicaré cómo funciona este método paso a paso.
Pasos para Implementar el Método de Monte Carlo
- Generar un número grande de puntos aleatorios dentro de un cuadrado que circunscribe el círculo.
- Contar cuántos de esos puntos caen dentro del círculo.
- Calcular el área del círculo utilizando la proporción de puntos dentro del círculo en relación con el total de puntos generados.
Para ilustrar esto con un ejemplo práctico, imagina que tienes un cuadrado de lado 2r y un círculo de radio r inscrito dentro de ese cuadrado. Al generar puntos aleatorios dentro del cuadrado, puedes contar cuántos de esos puntos caen dentro del círculo y utilizar esa proporción para aproximar el área del círculo.
Implementación Práctica del Método de Monte Carlo
Ahora que entendemos el concepto detrás del método de Monte Carlo, veamos cómo podemos implementarlo en código. A continuación, se muestra un ejemplo en Python, uno de los lenguajes de programación más utilizados para este tipo de simulaciones:
import random def calcular_area_circulo(n_puntos): puntos_dentro_circulo = 0 radio = 1 for _ in range(n_puntos): x = random.uniform(-radio, radio) y = random.uniform(-radio, radio) if x**2 + y**2 <= radio**2: puntos_dentro_circulo += 1 area_cuadrado = (2 * radio) ** 2 area_circulo = (puntos_dentro_circulo / n_puntos) * area_cuadrado return area_circulo n_puntos = 10000 area_estimada = calcular_area_circulo(n_puntos) print(f"El área estimada del círculo es: {area_estimada}")
En este código, generamos 10,000 puntos aleatorios y contamos cuántos de ellos caen dentro del círculo. Luego utilizamos esa proporción para calcular el área estimada del círculo.
Ventajas y Desventajas del Método de Monte Carlo
Como todo método, el método de Monte Carlo tiene sus ventajas y desventajas. A continuación, te presento algunas de las más destacadas:
Ventajas
- Fácil de implementar en código.
- Puede ser utilizado para calcular áreas de figuras geométricas complejas.
- Permite obtener una buena aproximación con una cantidad suficiente de puntos.
Desventajas
- Requiere una gran cantidad de puntos para obtener una alta precisión.
- Puede ser ineficiente para áreas muy pequeñas o muy grandes.
- Dependencia de la calidad de los números aleatorios generados.
Comparativa con Métodos Tradicionales
Es interesante comparar el método de Monte Carlo con los métodos tradicionales de cálculo del área de un círculo. El método tradicional utiliza la fórmula matemática directa, mientras que el método de Monte Carlo utiliza simulaciones. Ambos métodos tienen sus propios pros y contras, y la elección entre uno u otro depende del contexto y los recursos disponibles.
Método Tradicional
El método tradicional es rápido y preciso, ya que se basa en una fórmula matemática directa. Sin embargo, puede ser limitado cuando se trata de figuras geométricas más complejas.
Método de Monte Carlo
El método de Monte Carlo es más flexible y puede ser utilizado para figuras más complejas. Sin embargo, puede requerir una gran cantidad de puntos y recursos computacionales para obtener una alta precisión.
Aplicaciones del Método de Monte Carlo
El método de Monte Carlo no solo se utiliza para calcular el área de un círculo. Tiene una amplia gama de aplicaciones en diversos campos, incluyendo:
Finanzas
En finanzas, el método de Monte Carlo se utiliza para modelar y simular el comportamiento de los mercados financieros, permitiendo a los analistas evaluar riesgos y tomar decisiones informadas.
Ciencias Físicas
En las ciencias físicas, se utiliza para simular fenómenos complejos como la difusión de partículas y la interacción de radiación con la materia.
Ingeniería
En ingeniería, se aplica para optimizar diseños y evaluar la fiabilidad de sistemas y estructuras.
Conclusión: ¿Qué Método es Mejor?
La elección del método para calcular el área de un círculo depende del contexto y los recursos disponibles. El método de Monte Carlo ofrece flexibilidad y es útil para figuras geométricas complejas, mientras que el método tradicional es rápido y preciso para círculos simples. En cualquier caso, es importante entender las fortalezas y limitaciones de cada método para tomar decisiones informadas.
Espero que este artículo te haya proporcionado una comprensión clara y detallada sobre cómo calcular el área de un círculo mediante simulaciones. Si tienes alguna pregunta o deseas profundizar en algún aspecto, no dudes en consultar los recursos adicionales que he proporcionado a lo largo del artículo.
