Trigonometría: Todo lo que Necesitas Saber
Introducción a la Esférica y la Trigonometría
Hola, soy Leandro, y hoy vamos a sumergirnos en el fascinante mundo de la esférica y la trigonometría. Estos dos conceptos matemáticos son fundamentales en muchas áreas del conocimiento, desde la navegación hasta la astronomía. Si alguna vez te has preguntado qué son, en qué se diferencian y cuál es mejor, estás en el lugar correcto.
¿Qué es la Trigonometría?
Definición y Conceptos Básicos
La trigonometría es una rama de las matemáticas que estudia las relaciones entre los ángulos y los lados de los triángulos. Es una herramienta esencial para resolver problemas en geometría, física, ingeniería, y muchas otras disciplinas. Los conceptos básicos de la trigonometría incluyen:
- Ángulos
- Seno, coseno y tangente
- Funciones trigonométricas
- Identidades trigonométricas
Aplicaciones de la Trigonometría
La trigonometría tiene una amplia gama de aplicaciones prácticas. Por ejemplo, se utiliza en la construcción para determinar las pendientes de los techos, en la navegación para calcular las rutas, y en la astronomía para medir distancias entre estrellas. Si quieres profundizar más en este tema, puedes consultar este enlace.
¿Qué es la Esférica?
Definición y Conceptos Básicos
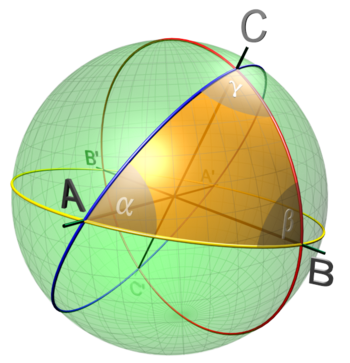
La esférica, también conocida como trigonometría esférica, es una rama de la trigonometría que se ocupa de los triángulos esféricos. Estos son triángulos formados por arcos de círculos máximos en una esfera, como los que se encuentran en la superficie de la Tierra. Los conceptos básicos de la esférica incluyen:
- Triángulos esféricos
- Ángulos diédricos
- Lados y ángulos esféricos
- Identidades esféricas
Aplicaciones de la Esférica
La esférica es crucial en campos como la astronomía, la geodesia y la navegación. Por ejemplo, los navegantes utilizan la trigonometría esférica para calcular las rutas más cortas entre dos puntos en la superficie de la Tierra. Si quieres aprender más, visita este enlace.
Diferencias entre Esférica y Trigonometría
Ámbito de Aplicación
La principal diferencia entre la esférica y la trigonometría plana radica en su ámbito de aplicación. Mientras que la trigonometría plana se ocupa de triángulos en un plano, la esférica se ocupa de triángulos en la superficie de una esfera.
Fórmulas y Cálculos
Las fórmulas utilizadas en la esférica son diferentes de las de la trigonometría plana. Por ejemplo, en un triángulo esférico, la suma de los ángulos internos es siempre mayor de 180 grados, a diferencia de los triángulos planos donde siempre es 180 grados.
Complejidad
La trigonometría esférica es generalmente considerada más compleja que la trigonometría plana debido a la naturaleza curva de la esfera. Esto hace que los cálculos sean más complicados y que se requiera un mayor nivel de precisión.
¿Cuál es Mejor: Esférica o Trigonometría Plana?
Depende del Contexto
La pregunta de cuál es mejor, si la esférica o la trigonometría plana, realmente depende del contexto en el que se utilicen. Si estás trabajando en un plano, la trigonometría plana es más adecuada. Sin embargo, si estás trabajando con superficies esféricas, como la Tierra, la esférica es imprescindible.
Complementariedad
Es importante entender que ambos tipos de trigonometría son complementarios. No es una cuestión de cuál es mejor, sino de cuál es más adecuada para el problema que estás tratando de resolver.
Competencia en el Nicho de Esférica y Trigonometría
Contenido Existente
Al investigar sobre la competencia en el nicho de esférica y trigonometría, me encontré con varios artículos y recursos en línea que abordan estos temas de manera detallada. Algunos de los más destacados incluyen:
- Artículo de Wikipedia sobre Trigonometría
- Artículo de Wikipedia sobre Trigonometría Esférica
- Cursos de Trigonometría en Khan Academy
- Recursos de Trigonometría en Maths is Fun
Análisis de la Competencia
La mayoría de los artículos y recursos que encontré son bastante técnicos y están dirigidos a un público que ya tiene un conocimiento básico de matemáticas. Mi objetivo con este artículo es hacerlo más accesible y fácil de entender, sin sacrificar la precisión y la profundidad del contenido.
Conclusión: Esférica y Trigonometría en la Vida Real
En resumen, tanto la esférica como la trigonometría plana son herramientas matemáticas esenciales que tienen aplicaciones en una amplia variedad de campos. La elección entre una y otra depende del contexto específico de tu problema. Espero que este artículo te haya ayudado a entender mejor estos conceptos y cómo se aplican en la vida real. Si tienes alguna pregunta o comentario, no dudes en dejarlo abajo. ¡Hasta la próxima!
