Guía Completa
Introducción a las Leyes de los Senos y Cosenos
¡Hola a todos! Me llamo Leandro y hoy quiero compartir con ustedes mi experiencia y conocimientos sobre las Leyes de los Senos y Cosenos. Estas leyes son fundamentales en la trigonometría y son herramientas poderosas que te ayudarán a resolver una gran variedad de problemas geométricos. Ya sea que estés en la escuela, en la universidad o simplemente quieras refrescar tus conocimientos, has llegado al lugar correcto.
¿Qué son las Leyes de los Senos y Cosenos?
Antes de profundizar en las diferencias y aplicaciones de estas leyes, es importante entender qué son y por qué son tan útiles.
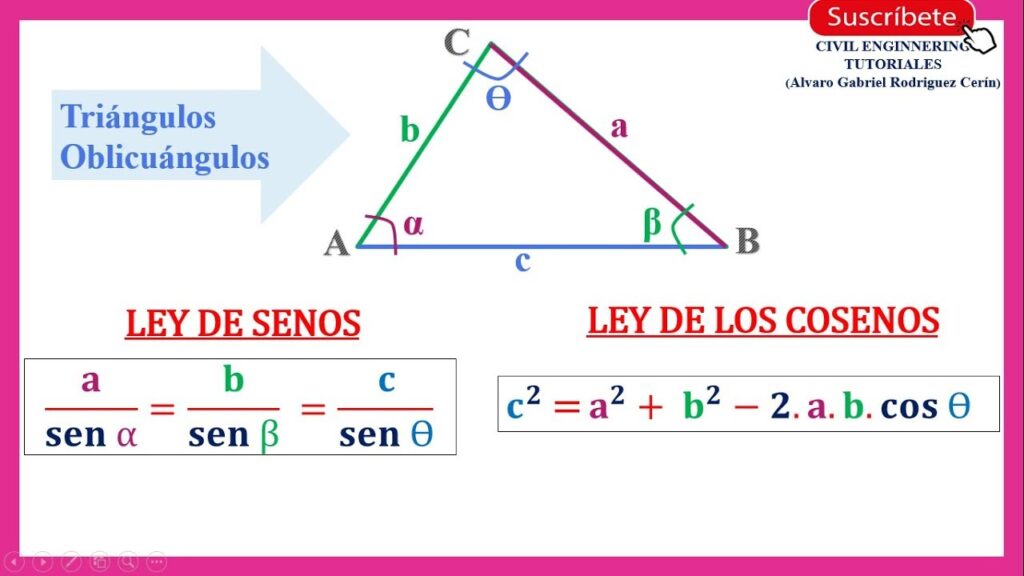
Ley de los Senos
La Ley de los Senos establece que en cualquier triángulo, la relación entre la longitud de un lado y el seno de su ángulo opuesto es constante para los tres lados del triángulo. Matemáticamente, se expresa de la siguiente manera:
a/sin(A) = b/sin(B) = c/sin(C)
Donde a, b y c son las longitudes de los lados del triángulo, y A, B y C son los ángulos opuestos a estos lados. Esta ley es especialmente útil para resolver triángulos que no son rectángulos.
Ley de los Cosenos
La Ley de los Cosenos es otra herramienta esencial en la trigonometría. Relaciona las longitudes de los lados de un triángulo con el coseno de uno de sus ángulos. Se expresa así:
c² = a² + b² – 2ab * cos(C)
Esta ley es particularmente útil para resolver triángulos cuando conocemos dos lados y el ángulo entre ellos, o cuando conocemos los tres lados del triángulo.
Aplicaciones de las Leyes de los Senos y Cosenos
Ahora que sabemos qué son las Leyes de los Senos y Cosenos, veamos algunas de sus aplicaciones prácticas.
Aplicaciones de la Ley de los Senos
La Ley de los Senos se utiliza comúnmente en situaciones donde conocemos dos ángulos y un lado (AAS o ASA) o dos lados y un ángulo opuesto (SSA). Algunas aplicaciones típicas incluyen:
- Determinar la distancia entre dos puntos en navegación y geografía.
- Resolver problemas de física relacionados con vectores y fuerzas.
- Calcular ángulos y distancias en arquitectura e ingeniería.
Aplicaciones de la Ley de los Cosenos
La Ley de los Cosenos es especialmente útil cuando conocemos dos lados y el ángulo entre ellos (SAS) o los tres lados del triángulo (SSS). Algunas aplicaciones incluyen:
- Calcular la distancia entre dos puntos en un espacio tridimensional.
- Resolver problemas de mecánica y dinámica en física.
- Diseñar estructuras y componentes en ingeniería civil y mecánica.
Diferencias entre la Ley de los Senos y la Ley de los Cosenos
Una pregunta común es: ¿cuál es la diferencia entre la Ley de los Senos y la Ley de los Cosenos, y cuándo deberíamos usar una sobre la otra? Aquí hay algunas pautas para ayudarte a decidir:
Cuándo usar la Ley de los Senos
Usa la Ley de los Senos cuando conoces:
- Dos ángulos y un lado (AAS o ASA).
- Dos lados y un ángulo opuesto (SSA).
Esta ley es más simple de aplicar en estos casos y te permitirá encontrar las longitudes y ángulos restantes del triángulo.
Cuándo usar la Ley de los Cosenos
Usa la Ley de los Cosenos cuando conoces:
- Dos lados y el ángulo entre ellos (SAS).
- Los tres lados del triángulo (SSS).
Esta ley es más adecuada para estos casos, ya que te permitirá calcular ángulos y longitudes con precisión.
Ejemplos Prácticos de las Leyes de los Senos y Cosenos
Para entender mejor cómo aplicar estas leyes, veamos algunos ejemplos prácticos.
Ejemplo de la Ley de los Senos
Imagina que tienes un triángulo con los siguientes datos:
- Ángulo A = 30°
- Ángulo B = 45°
- Lado a = 10 cm
Queremos encontrar el lado b. Usamos la Ley de los Senos:
a/sin(A) = b/sin(B)
Sustituimos los valores conocidos:
10/sin(30°) = b/sin(45°)
Calculamos los senos de los ángulos:
10/0.5 = b/0.707
Finalmente, resolvemos para b:
b = 10 * 0.707 / 0.5 = 14.14 cm
Ejemplo de la Ley de los Cosenos
Imagina que tienes un triángulo con los siguientes datos:
- Lado a = 7 cm
- Lado b = 10 cm
- Ángulo C = 60°
Queremos encontrar el lado c. Usamos la Ley de los Cosenos:
c² = a² + b² – 2ab * cos(C)
Sustituimos los valores conocidos:
c² = 7² + 10² – 2*7*10 * cos(60°)
Calculamos el coseno del ángulo:
cos(60°) = 0.5
Entonces:
c² = 49 + 100 – 70
c² = 79
Finalmente, tomamos la raíz cuadrada para encontrar c:
c = √79 ≈ 8.89 cm
Comparación de las Leyes de los Senos y Cosenos
A menudo surge la pregunta de cuál de estas dos leyes es «mejor». La respuesta depende del contexto y de los datos que tengas disponibles.
Ventajas de la Ley de los Senos
- Más simple de aplicar cuando se conocen dos ángulos y un lado, o dos lados y un ángulo opuesto.
- Útil para resolver triángulos no rectángulos.
Ventajas de la Ley de los Cosenos
- Más versátil para resolver triángulos con dos lados y el ángulo entre ellos, o los tres lados.
- Permite calcular distancias y ángulos con mayor precisión en geometría tridimensional.
Recursos Adicionales y Enlaces Relacionados
Para aquellos que deseen profundizar más en el tema de las Leyes de los Senos y Cosenos, aquí hay algunos recursos adicionales:
Conclusión
Espero que este artículo te haya ayudado a entender mejor las Leyes de los Senos y Cosenos. Como hemos visto, ambas leyes son herramientas poderosas que nos permiten resolver una amplia variedad de problemas geométricos y trigonométricos. La clave está en saber cuándo y cómo aplicarlas de manera efectiva.
Si tienes alguna pregunta o comentario, no dudes en dejarlo abajo. ¡Estoy aquí para ayudarte!
