Las Razones Trigonométricas – Explicación
Introducción a las Razones Trigonométricas: ¿Qué son y para qué sirven?
Hola, soy Leandro, y hoy vamos a sumergirnos en el fascinante mundo de las razones trigonométricas. Quizás te suene a algo complejo y aburrido, pero te aseguro que entender estas razones puede ser mucho más interesante de lo que piensas. Si eres estudiante, profesor o simplemente alguien curioso, este artículo te servirá para comprender qué son, cómo funcionan y por qué son tan importantes en matemáticas y en la vida real.
¿Qué son las Razones Trigonométricas?
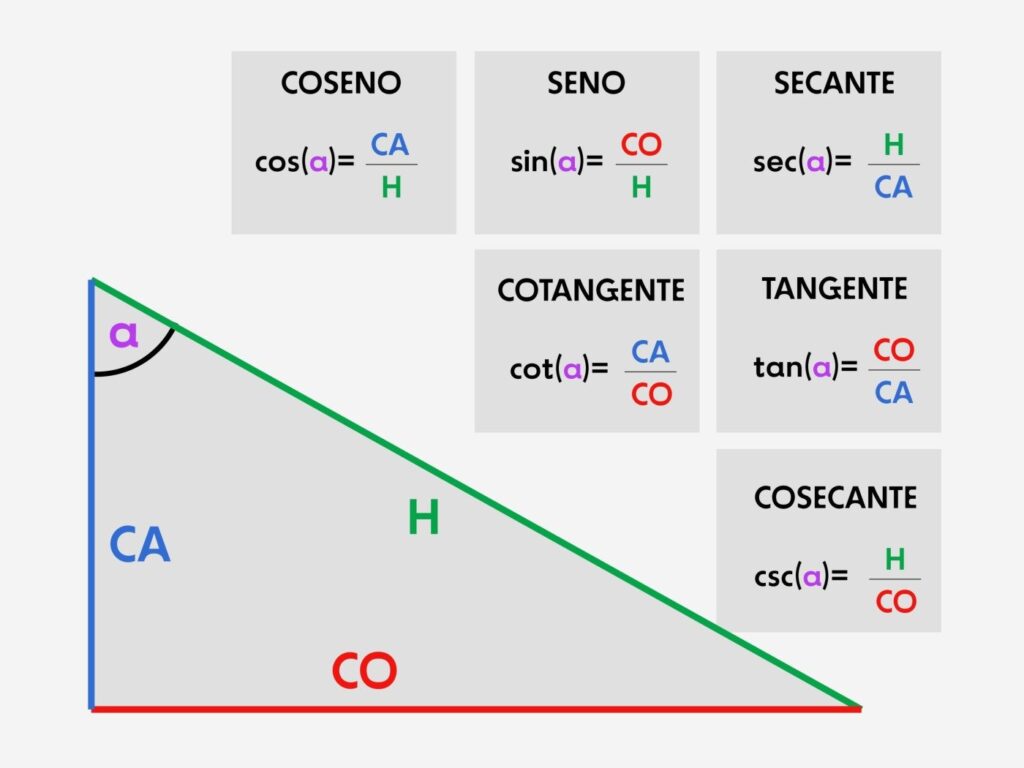
Las razones trigonométricas, también conocidas como funciones trigonométricas, son relaciones matemáticas que se establecen entre los ángulos y los lados de un triángulo rectángulo. Las tres funciones más conocidas son el seno, el coseno y la tangente. Para ser más preciso:
- Seno (sin): Es la razón entre el cateto opuesto al ángulo y la hipotenusa.
- Coseno (cos): Es la razón entre el cateto adyacente al ángulo y la hipotenusa.
- Tangente (tan): Es la razón entre el cateto opuesto al ángulo y el cateto adyacente.
Estas funciones son fundamentales en la trigonometría y tienen aplicaciones en diversas disciplinas como la física, la ingeniería y la informática.
Aplicaciones de las Razones Trigonométricas en la Vida Real
Ahora que ya sabes qué son las razones trigonométricas, hablemos de cómo se aplican en la vida real. Por ejemplo, en la construcción y la arquitectura, las funciones trigonométricas son esenciales para calcular ángulos y distancias. Los ingenieros las utilizan para diseñar puentes y edificios, asegurándose de que las estructuras sean seguras y estables.
Otra aplicación fascinante es en la navegación. Los navegantes utilizan las razones trigonométricas para determinar su posición exacta en el mar, calculando ángulos y distancias con la ayuda de sextantes y otros instrumentos.
Cómo Calcular las Razones Trigonométricas
Vamos a entrar en materia práctica. ¿Cómo se calculan las razones trigonométricas? Aquí te dejo los pasos básicos:
Cálculo del Seno
Para calcular el seno de un ángulo, simplemente divide la longitud del cateto opuesto al ángulo entre la longitud de la hipotenusa.
sin(θ) = cateto opuesto / hipotenusa
Cálculo del Coseno
Para calcular el coseno de un ángulo, divide la longitud del cateto adyacente al ángulo entre la longitud de la hipotenusa.
cos(θ) = cateto adyacente / hipotenusa
Cálculo de la Tangente
Para calcular la tangente de un ángulo, divide la longitud del cateto opuesto al ángulo entre la longitud del cateto adyacente.
tan(θ) = cateto opuesto / cateto adyacente
Funciones Trigonométricas Inversas
Además de las funciones trigonométricas básicas, también existen sus inversas: arcseno, arcocoseno y arcotangente. Estas funciones se utilizan para encontrar el ángulo cuando ya conocemos las razones trigonométricas.
Arcseno (asin)
El arcseno es la función inversa del seno y se utiliza para encontrar el ángulo cuyo seno es un valor dado.
θ = asin(valor)
Arcocoseno (acos)
El arcocoseno es la función inversa del coseno y se utiliza para encontrar el ángulo cuyo coseno es un valor dado.
θ = acos(valor)
Arcotangente (atan)
La arcotangente es la función inversa de la tangente y se utiliza para encontrar el ángulo cuya tangente es un valor dado.
θ = atan(valor)
Razones Trigonométricas en el Plano Cartesiano
Las razones trigonométricas también se pueden aplicar en el plano cartesiano, lo que nos permite trabajar con coordenadas y vectores. Imagina que tienes un punto P con coordenadas (x, y) en el plano.
El radio vector que une el origen con el punto P forma un ángulo θ con el eje x. En este caso:
- Seno: y / r
- Coseno: x / r
- Tangente: y / x
donde r es la distancia del origen al punto P, calculada como:
r = √(x² + y²)
Ejemplos Prácticos de Uso de Razones Trigonométricas
Vamos a ver algunos ejemplos prácticos para que entiendas mejor cómo se aplican las razones trigonométricas:
Ejemplo 1: Calcular la Altura de un Edificio
Supongamos que quieres calcular la altura de un edificio, y sabes que desde un punto a 50 metros de la base del edificio, el ángulo de elevación al tope del edificio es de 30 grados. Usando la tangente:
tan(30°) = altura / 50 altura = 50 * tan(30°) altura ≈ 28.87 metros
Ejemplo 2: Distancia en el Plano Cartesiano
Si tienes dos puntos en el plano cartesiano, P1(3, 4) y P2(7, 1), y quieres calcular la distancia entre ellos, puedes usar el teorema de Pitágoras y las razones trigonométricas:
distancia = √((7 - 3)² + (1 - 4)²) distancia ≈ 5 metros
Comparación de las Razones Trigonométricas con Otras Funciones Matemáticas
Es importante también entender cómo las razones trigonométricas se comparan con otras funciones matemáticas. A diferencia de las funciones lineales o cuadráticas, las funciones trigonométricas son periódicas, lo que significa que se repiten en intervalos regulares. Esto las hace especialmente útiles para modelar fenómenos cíclicos como las ondas sonoras y las señales eléctricas.
Recursos y Enlaces Relacionados
Para profundizar más en el tema, aquí te dejo algunos enlaces útiles:
Conclusión
Espero que este artículo te haya ayudado a entender mejor qué son las razones trigonométricas y cómo se aplican en diferentes contextos. Desde la construcción hasta la navegación, estas funciones matemáticas son herramientas poderosas que nos ayudan a resolver problemas complejos de manera más sencilla. Si tienes alguna pregunta o quieres compartir tu experiencia, no dudes en dejar un comentario. ¡Hasta la próxima!
