Guía Completa
Introducción a las Funciones Trigonométricas
¡Hola a todos! Soy Leandro, y hoy quiero hablarles sobre un tema que, aunque puede parecer complicado, es fundamental en el mundo de las matemáticas: las funciones trigonométricas. Desde mi experiencia enseñando trigonometría, he encontrado que entender estas funciones puede abrir la puerta a innumerables aplicaciones tanto en la vida diaria como en diversas disciplinas científicas.
¿Qué son las Funciones Trigonométricas?
Las funciones trigonométricas son funciones matemáticas que relacionan los ángulos de un triángulo con las longitudes de sus lados. Estas funciones son esenciales en el estudio de los triángulos y en la modelización de fenómenos periódicos, como las ondas.
Tipos de Funciones Trigonométricas
Existen varias funciones trigonométricas, pero las más conocidas son:
- Seno (sin)
- Coseno (cos)
- Tangente (tan)
- Cosecante (csc)
- Secante (sec)
- Cotangente (cot)
El Seno y el Coseno: Dos Funciones Trigonométricas Fundamentales
El seno y el coseno son quizás las funciones trigonométricas más conocidas. Estas funciones se definen en el contexto de un triángulo rectángulo, y tienen aplicaciones que van desde la física hasta la ingeniería.
Seno (sin)
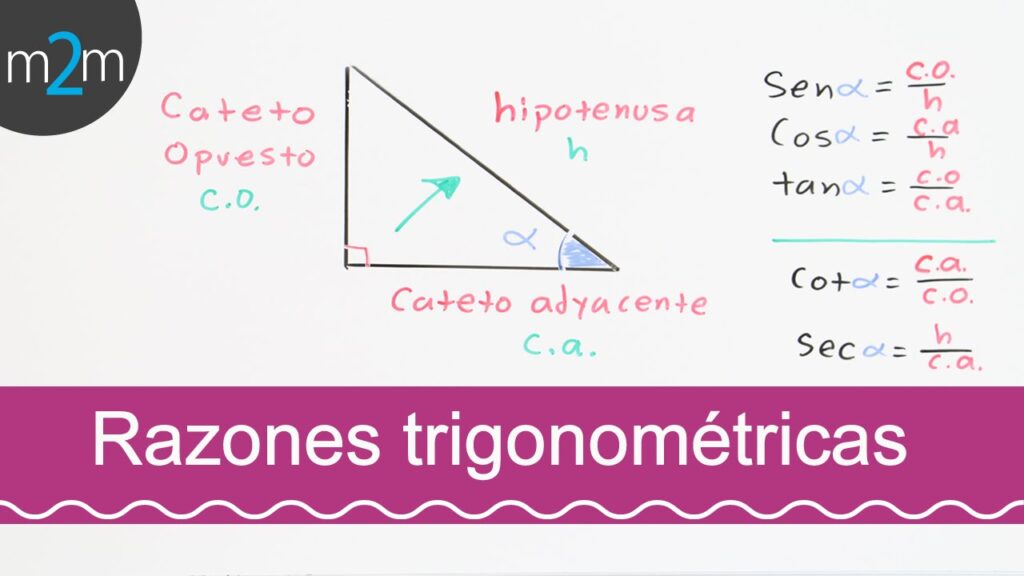
El seno de un ángulo se define como la longitud del cateto opuesto al ángulo dividido por la longitud de la hipotenusa. Matemáticamente, esto se expresa como:
sin(θ)=ah
Coseno (cos)
El coseno de un ángulo se define como la longitud del cateto adyacente al ángulo dividido por la longitud de la hipotenusa. Matemáticamente, esto se expresa como:
cos(θ)=bh
Aplicaciones de las Funciones Trigonométricas
Las funciones trigonométricas tienen una amplia gama de aplicaciones en diversos campos. Aquí les dejo algunas de las más comunes:
Física
En física, las funciones trigonométricas son esenciales para describir fenómenos ondulatorios, como las ondas sonoras y las ondas electromagnéticas. También se utilizan en el estudio de movimientos periódicos, como el movimiento armónico simple.
Ingeniería
En ingeniería, las funciones trigonométricas se utilizan para analizar y diseñar estructuras, circuitos eléctricos, y sistemas de control. Por ejemplo, en la ingeniería civil, se utilizan para calcular las fuerzas en puentes y edificios.
Astronomía
En astronomía, estas funciones se utilizan para calcular las posiciones de las estrellas y planetas, y para entender las órbitas de los cuerpos celestes.
Navegación
En navegación, las funciones trigonométricas se utilizan para determinar la posición y el rumbo de un barco o avión en relación con puntos de referencia conocidos.
Diferencias entre las Funciones Trigonométricas
Una pregunta común que suele surgir es: ¿Cuál es la diferencia entre las diversas funciones trigonométricas? La respuesta reside principalmente en cómo se definen estas funciones en relación con los lados de un triángulo rectángulo.
Diferencias entre Seno y Coseno
El seno se relaciona con el cateto opuesto al ángulo, mientras que el coseno se relaciona con el cateto adyacente. Ambos se dividen por la hipotenusa.
Diferencias entre Tangente y Cotangente
La tangente de un ángulo se define como la relación entre el seno y el coseno de ese ángulo. Por otro lado, la cotangente es la inversa de la tangente.
Diferencias entre Secante y Cosecante
La secante de un ángulo es la inversa del coseno, mientras que la cosecante es la inversa del seno.
Funciones Trigonométricas: Gráficas y Propiedades
Las gráficas de las funciones trigonométricas son herramientas muy útiles para visualizar cómo varían estas funciones con el ángulo. Aquí les dejo un breve resumen de las características de las gráficas de las funciones más comunes.
Gráfica del Seno
La gráfica del seno es una onda sinusoidal que oscila entre -1 y 1. Tiene un periodo de 2π y es simétrica respecto al origen.
Gráfica del Coseno
La gráfica del coseno también es una onda sinusoidal, pero está desplazada 90 grados respecto a la del seno. También oscila entre -1 y 1 y tiene un periodo de 2π.
Gráfica de la Tangente
La gráfica de la tangente tiene una forma diferente, con asíntotas verticales en los puntos donde el coseno es cero. Oscila entre -∞ y ∞ y tiene un periodo de π.
Conclusión: La Importancia de las Funciones Trigonométricas
En resumen, las funciones trigonométricas son herramientas matemáticas esenciales con aplicaciones en una amplia variedad de campos. Desde la física hasta la astronomía, pasando por la ingeniería y la navegación, estas funciones nos permiten modelar y entender fenómenos complejos de una manera simple y elegante.
Si desean profundizar más en este tema, les recomiendo revisar algunos recursos adicionales que pueden encontrar en Internet. Aquí les dejo algunos enlaces útiles:
