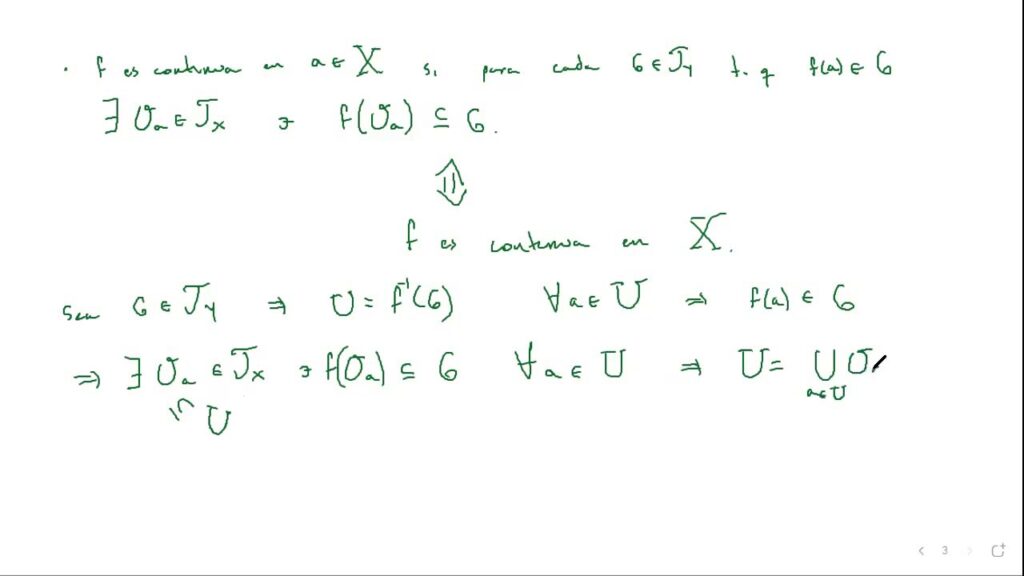
Topología Funciones Continuas

¡Hola a todos! Soy Leandro, y hoy quiero hablarles de un tema fascinante en el mundo de las matemáticas: la Topología de Funciones Continuas. Quizás suene un poco complejo al principio, pero les aseguro que, con un enfoque desenfadado y basado en mi experiencia, lo entenderán de maravilla.

Conoce más sobre: Topología

¿Qué vas a encontrar aquí?

Introducción a la Topología

Para empezar, hablemos de qué es la topología. En términos simples, la topología es una rama de las matemáticas que estudia las propiedades de los espacios que se mantienen a través de deformaciones continuas, como estiramientos y doblamientos, pero no desgarros ni pegados. ¿Han oído hablar del famoso ejemplo de la taza y el donut? En topología, ambos son considerados equivalentes porque pueden transformarse uno en el otro sin cortar ni pegar.

¿Qué son las Funciones Continuas?

Ahora, antes de sumergirnos en la combinación de estos dos conceptos, aclaremos qué son las funciones continuas. En matemáticas, una función continua es aquella en la que pequeñas variaciones en la entrada resultan en pequeñas variaciones en la salida. Si alguna vez han dibujado una gráfica sin levantar el lápiz del papel, ¡eso es una función continua!

La Unión de Topología y Funciones Continuas

Cuando unimos la topología con las funciones continuas, estudiamos cómo se comportan estas funciones dentro de los espacios topológicos. La continuidad de una función en topología se define de manera similar a la continuidad en el cálculo, pero utilizando el concepto de vecindades (o entornos) en lugar de límites. Una función $f: X \to Y$ es continua si para cada conjunto abierto $V$ en $Y$ , el conjunto preimagen $f^{-1}(V)$ es un conjunto abierto en $X$ .

Conoce tambien: Optimización en Negocios

Funciones Continuas en Espacios Topológicos.

Ejemplos y Aplicaciones

Ejemplo 1: Función Identidad

Un ejemplo sencillo es la función identidad $id_X: X \to X$ , donde $id_X(x) = x$ para todo $x$ en $X$ . Es trivialmente continua porque la preimagen de cualquier conjunto abierto es el mismo conjunto, que es abierto por definición.

Ejemplo 2: Funciones Constantes

Otro ejemplo fácil son las funciones constantes. Si $c \in Y$ es un valor fijo, la función $f: X \to Y$ definida por $f(x) = c$ para todo $x \in X$ es continua. La preimagen de cualquier conjunto que no contiene $c$ es el conjunto vacío (que es abierto), y la preimagen de cualquier conjunto que contiene $c$ es $X$ (que también es abierto).

Ejemplo 3: Función Cuadrática

Consideren la función cuadrática $f(x) = x^2$ en los números reales $\mathbb{R}$ . Esta función es continua en todo $\mathbb{R}$ porque los valores de $f(x)$ cambian de manera suave y continua a medida que $x$ varía.

Propiedades Importantes

Homeomorfismos

Una de las nociones clave en topología es la de homeomorfismo. Dos espacios topológicos $X$ y $Y$ son homeomorfos si existe una función continua bijectiva $f: X \to Y$ con una inversa también continua. Esto significa que $X$ y $Y$ son «topológicamente equivalentes», aunque pueden parecer diferentes a simple vista. Un homeomorfismo preserva las propiedades topológicas esenciales.

Espacios Compactos y Conexos

Otra propiedad importante es la de los espacios compactos. Un espacio topológico es compacto si cada recubrimiento abierto tiene un subrecubrimiento finito. Las funciones continuas tienen una propiedad interesante: si $X$ es compacto y $f: X \to Y$ es continua, entonces $f(X)$ es compacto en $Y$ .

Los espacios conexos son aquellos que no pueden ser divididos en dos conjuntos abiertos disjuntos no vacíos. Una función continua mantiene la conexión: la imagen de un espacio conexo bajo una función continua también es conexa.

Conclusión

Espero que este viaje por la Topología de Funciones Continuas haya sido tan interesante para ustedes como lo es para mí. Desde las definiciones básicas hasta las aplicaciones más complejas, hemos cubierto mucho terreno. Recuerden que la topología es una herramienta poderosa en matemáticas, y entender las funciones continuas dentro de este marco puede abrir muchas puertas a nuevas ideas y aplicaciones.

Conoce tambien: Derivadas

Recursos Adicionales

Para aquellos interesados en profundizar más, les recomiendo explorar libros de texto de topología general y recursos en línea como cursos de matemáticas avanzadas y artículos académicos. Siempre hay más por aprender, y la topología es un campo en constante evolución con muchas áreas fascinantes por descubrir.

Si tienen preguntas o quieren discutir más sobre este tema, no duden en dejar sus comentarios. ¡Hasta la próxima!