Raíces Cuadradas: Un Viaje Matemático con Leandro
Introducción: ¿Qué es una raíz cuadrada?
¡Hola, amigos matemáticos! Soy Leandro, y hoy vamos a sumergirnos en el maravilloso mundo de las raíces cuadradas. ¿Sabías que las raíces cuadradas son esenciales en muchas áreas de las matemáticas y las ciencias? No te preocupes, te llevaré de la mano para que entendamos todo sobre ellas.
Definición de raíz cuadrada
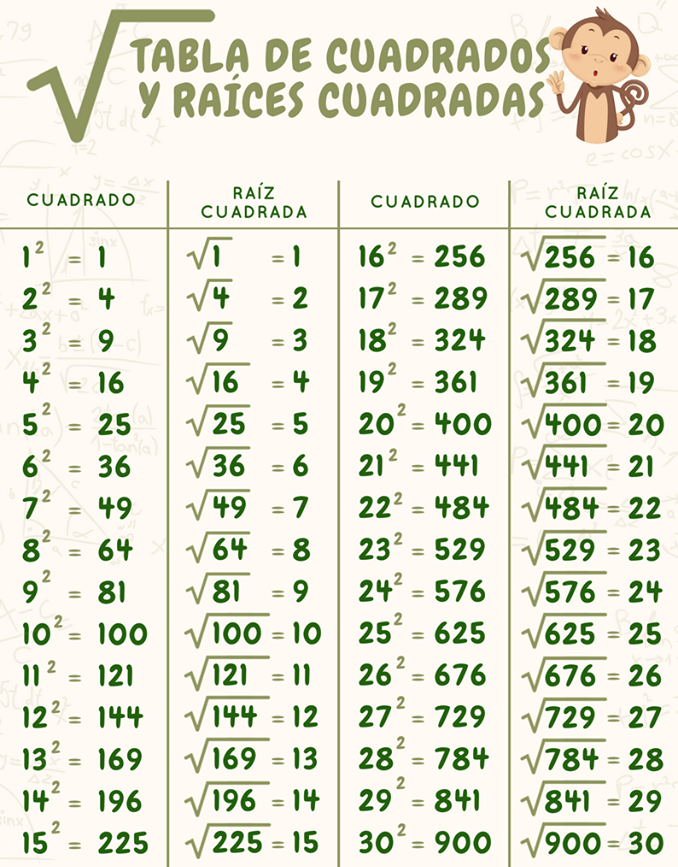
Empecemos por lo básico. La raíz cuadrada de un número es otro número que, al multiplicarse por sí mismo, da como resultado el número original. Por ejemplo, la raíz cuadrada de 9 es 3, porque 3 x 3 = 9.
Historia de las raíces cuadradas
Las raíces cuadradas tienen una historia fascinante. Los antiguos babilonios ya las usaban hace más de 4000 años. Ellos tenían métodos bastante ingeniosos para aproximar raíces cuadradas. Más adelante, los griegos, especialmente Euclides, también hicieron grandes avances en este campo.
Cómo calcular una raíz cuadrada
Método tradicional
El método más tradicional para calcular raíces cuadradas es la factorización. Si puedes descomponer un número en sus factores primos, puedes encontrar su raíz cuadrada. Por ejemplo, para calcular la raíz cuadrada de 36, descomponemos 36 en 2 x 2 x 3 x 3. Luego, agrupamos los factores en pares: (2 x 3) x (2 x 3) = 6 x 6. Así, la raíz cuadrada de 36 es 6.
Algoritmo de la raíz cuadrada
También existe un algoritmo para calcular raíces cuadradas manualmente, parecido a la división larga. Este método es menos conocido, pero muy efectivo.
Calculadoras y software
Hoy en día, lo más común es usar calculadoras o software para calcular raíces cuadradas. Herramientas como WolframAlpha o calculadoras científicas facilitan este proceso enormemente.
Aplicaciones de las raíces cuadradas
Las raíces cuadradas tienen aplicaciones en diversas áreas. Desde la física hasta la economía, pasando por la ingeniería y, por supuesto, las matemáticas puras. Por ejemplo, en física se usan para calcular la velocidad de escape de un planeta. En estadística, se emplean en la fórmula de la desviación estándar.
Raíces cuadradas en el álgebra
En álgebra, las raíces cuadradas son fundamentales para resolver ecuaciones cuadráticas. Estas ecuaciones tienen la forma ax² + bx + c = 0. La fórmula cuadrática, que es -b ± √(b² – 4ac) / 2a, incluye una raíz cuadrada para encontrar las soluciones.
Raíces cuadradas en la geometría
En geometría, las raíces cuadradas se usan para calcular la longitud de los lados de un triángulo rectángulo mediante el teorema de Pitágoras. La fórmula es a² + b² = c², donde c es la hipotenusa. Así, c = √(a² + b²).
Raíces cuadradas en la vida cotidiana
Quizás no lo notes, pero las raíces cuadradas están presentes en nuestra vida diaria. Desde calcular el tamaño de una pantalla de televisión, hasta determinar la dosis de un medicamento, las raíces cuadradas son herramientas esenciales.
Comparación con otras operaciones matemáticas
Las raíces cuadradas son solo una de las muchas operaciones matemáticas que usamos. Comparadas con otras, como la suma, la resta o la multiplicación, las raíces cuadradas pueden parecer más complicadas. Sin embargo, con práctica y paciencia, cualquiera puede dominarlas.
Conclusión: La importancia de las raíces cuadradas
En resumen, las raíces cuadradas son una herramienta matemática esencial con aplicaciones en diversas áreas. Desde su historia antigua hasta sus usos modernos, estas operaciones nos ayudan a entender mejor el mundo que nos rodea.
