Los Números Reales: Una Guía Completa
Introducción a los Números Reales
¡Hola a todos! Soy Leandro y hoy quiero hablarles de un tema que puede parecer complicado, pero que en realidad es fascinante: los números reales. Durante años he trabajado con ellos, tanto en mi carrera profesional como en mi vida cotidiana, y quiero compartir con ustedes lo que he aprendido.
¿Qué Son los Números Reales?
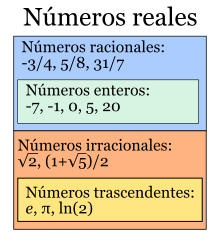
Los números reales son aquellos que podemos encontrar en la recta numérica. Incluyen a los números racionales (como 1/2, 4, -3) y a los números irracionales (como √2, π). Básicamente, cualquier número que podamos imaginar, excepto los números complejos, es un número real.
Si quieres una definición más técnica, los números reales son los elementos del conjunto R que incluyen todos los números racionales e irracionales. Estos números tienen la propiedad de que pueden ser representados como secuencias convergentes de números racionales.
Tipos de Números Reales
Números Racionales
Los números racionales son aquellos que pueden expresarse como una fracción de dos números enteros, donde el denominador no es cero. Ejemplos comunes son 1/2, -3/4, y 5. Si el número puede escribirse como una fracción simple, es racional.
Números Irracionales
Los números irracionales, por otro lado, no pueden expresarse como una fracción de dos números enteros. Ejemplos de estos números son π, e, y √2. Estos números tienen decimales infinitos que no se repiten.
Historia de los Números Reales
El concepto de los números reales ha evolucionado a lo largo de la historia. Desde los antiguos griegos hasta los matemáticos modernos, el entendimiento de estos números ha pasado por diversas etapas.
Antigua Grecia
En la antigua Grecia, los matemáticos como Pitágoras y Euclides ya estaban familiarizados con los números racionales y algunos irracionales, aunque no los entendían completamente. La famosa paradoja de la raíz de 2 (√2) fue un problema que los griegos no pudieron resolver fácilmente.
Edad Media y Renacimiento
Durante la Edad Media y el Renacimiento, el estudio de los números irracionales continuó, aunque de manera limitada. Fue en esta época cuando matemáticos como Fibonacci comenzaron a explorar más a fondo las propiedades de los números.
Era Moderna
En la era moderna, matemáticos como Cantor y Dedekind hicieron grandes avances en la comprensión de los números reales, desarrollando la teoría de conjuntos y la construcción de los números reales a partir de los racionales.
Propiedades de los Números Reales
Los números reales tienen varias propiedades interesantes que los hacen únicos y útiles en matemáticas.
Propiedad de Compleción
Una de las propiedades más importantes de los números reales es que son «completos». Esto significa que no hay «huecos» en la recta numérica. Cualquier número que podamos imaginar, ya sea racional o irracional, tiene un lugar en la recta numérica.
Propiedad de Densidad
Otra propiedad interesante es la densidad. Entre dos números reales cualesquiera, siempre hay otro número real. Esto significa que la recta numérica es infinitamente divisible.
Aplicaciones de los Números Reales
Los números reales son fundamentales en muchas áreas de la ciencia y la ingeniería. Aquí hay algunas aplicaciones de estos números en el mundo real.
Física
En física, los números reales son utilizados para medir cantidades como la velocidad, la aceleración y la energía. Sin los números reales, sería imposible describir muchos fenómenos físicos con precisión.
Ingeniería
En ingeniería, los números reales son utilizados en el diseño y análisis de sistemas. Desde la construcción de puentes hasta el diseño de circuitos electrónicos, los números reales juegan un papel crucial.
Economía
En economía, los números reales son utilizados para medir cantidades como el PIB, la inflación y el desempleo. Estos números nos permiten entender mejor la economía y tomar decisiones informadas.
Cómo Diferenciar Entre Números Reales y Otros Tipos de Números
Es importante saber cómo diferenciar los números reales de otros tipos de números, como los números complejos y los números imaginarios.
Números Complejos
Los números complejos incluyen una parte real y una parte imaginaria. Por ejemplo, el número complejo 3 + 4i tiene una parte real (3) y una parte imaginaria (4i). Los números reales no tienen una parte imaginaria.
Números Imaginarios
Los números imaginarios son aquellos que incluyen la unidad imaginaria «i», que es igual a la raíz cuadrada de -1. Un número imaginario puro no tiene una parte real. Ejemplos de números imaginarios son 2i y -5i.
Recursos Adicionales
Si quieres aprender más sobre los números reales, aquí te dejo algunos recursos adicionales que pueden ser de gran ayuda:
Conclusión
Los números reales son una parte fundamental de las matemáticas y tienen aplicaciones en muchas áreas de la ciencia y la ingeniería. Espero que este artículo te haya ayudado a entender mejor qué son los números reales y por qué son tan importantes.
