Todo lo que Necesitas Saber
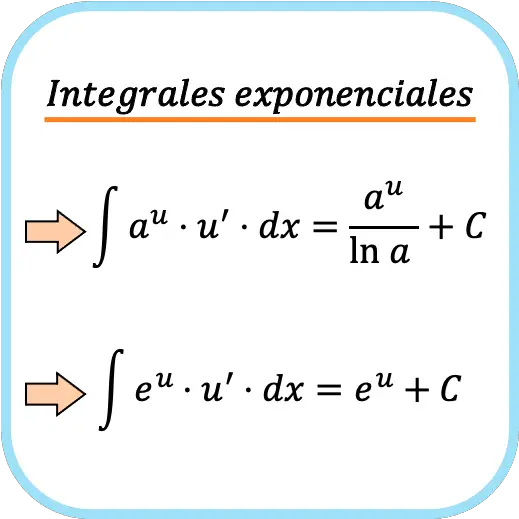
Introducción a las Integrales Exponenciales
¡Hola! Soy Leandro y hoy vamos a sumergirnos en el fascinante mundo de las integrales exponenciales. A lo largo de mi carrera como matemático y educador, he tenido la oportunidad de explorar este tema desde diversas perspectivas, y quiero compartir contigo todo lo que he aprendido.
Las integrales exponenciales son una clase especial de integrales donde la función a integrar incluye una expresión exponencial. Puede parecer intimidante al principio, pero no te preocupes, ¡estoy aquí para desglosarlo paso a paso!
¿Qué son las Integrales Exponenciales?
Vamos a empezar con lo básico. Una integral exponencial es una integral en la que el integrando (la función que estamos integrando) contiene una función exponencial, es decir, una función de la forma e^{x}, e^{-x}, o similares.
Para dar un ejemplo sencillo, considera la integral:
∫ e^x dx
Esta es una integral exponencial clásica y su solución es bastante directa: e^x + C, donde C es la constante de integración.
Tipos Comunes de Integrales Exponenciales
Hay varios tipos de integrales exponenciales que se presentan comúnmente en el cálculo y análisis matemático. Vamos a explorar algunos de los más importantes:
Integrales de la Forma ∫ e^x dx
Como mencionamos anteriormente, la integral de e^x es simplemente e^x + C. Esta es una de las integrales más básicas y una buena forma de iniciar nuestro estudio.
Integrales de la Forma ∫ e^{-x} dx
Para la integral de e^{-x}, utilizamos una técnica similar. La antiderivada de e^{-x} es -e^{-x} + C.
Integrales con Multiplicadores
Consideremos la integral ∫ e^{kx} dx, donde k es una constante. La solución a esta integral es (1/k) e^{kx} + C. Este patrón es útil para resolver integrales exponenciales más complejas.
Aplicaciones de las Integrales Exponenciales
Las integrales exponenciales no son solo un ejercicio académico; tienen aplicaciones prácticas en diversas áreas. Aquí te presento algunas de las más relevantes:
Física
En física, las integrales exponenciales se utilizan para modelar fenómenos como el decaimiento radiactivo y el crecimiento poblacional. Por ejemplo, la ley de desintegración radiactiva se basa en una función exponencial.
Economía
En economía, estas integrales se aplican en modelos de crecimiento económico y cálculos de interés compuesto. Los economistas utilizan funciones exponenciales para predecir el comportamiento futuro de variables económicas.
Ingeniería
Los ingenieros utilizan integrales exponenciales en el análisis de circuitos eléctricos y en el estudio de la transferencia de calor. Estas integrales ayudan a modelar la respuesta de sistemas bajo ciertas condiciones.
Técnicas para Resolver Integrales Exponenciales
Existen varias técnicas para resolver integrales exponenciales. Aquí te presento algunas de las más útiles:
Integración por Partes
La técnica de integración por partes es muy útil para resolver integrales exponenciales más complejas. La fórmula básica es:
∫ u dv = uv - ∫ v du
Donde u y dv son partes de la integral original.
Sustitución
Otro método común es la sustitución. Esta técnica es especialmente útil cuando la integral contiene una función compuesta. Por ejemplo, para resolver ∫ e^{2x} dx, podemos hacer una sustitución u = 2x. Esto simplifica la integral y facilita su resolución.
Comparación con Otras Integrales
Las integrales exponenciales tienen características únicas que las distinguen de otros tipos de integrales. Vamos a compararlas con algunos otros tipos comunes:
Integrales Polinomiales
Las integrales de polinomios, como ∫ x^n dx, son generalmente más simples de resolver que las integrales exponenciales. Sin embargo, las integrales exponenciales tienen aplicaciones más diversas y pueden modelar una gama más amplia de fenómenos.
Integrales Trigonométricas
Las integrales que involucran funciones trigonométricas, como ∫ sin(x) dx, tienen técnicas de resolución diferentes y a menudo requieren el uso de identidades trigonométricas. Las integrales exponenciales son generalmente más directas, aunque pueden ser más complicadas en casos específicos.
Recursos Adicionales
Si quieres profundizar más en el estudio de las integrales exponenciales, aquí te dejo algunos recursos útiles:
Competencia en el Nicho
Al investigar la competencia en el nicho de las integrales exponenciales, encontré varios sitios web y recursos que abordan este tema. Algunos de los más destacados incluyen:
- Integrales.com: Integrales Exponenciales
- Superprof: Integrales Exponenciales
- Matemáticas.net: Integrales Exponenciales
Estos recursos son muy completos y ofrecen una gran cantidad de ejemplos y ejercicios prácticos. Te recomiendo que los visites para complementar lo que hemos discutido aquí.
Conclusión
Las integrales exponenciales son una herramienta poderosa en el cálculo y tienen aplicaciones en diversas disciplinas. Aunque pueden parecer complicadas al principio, con práctica y las técnicas adecuadas, puedes dominarlas.
Espero que este artículo te haya sido útil y que ahora tengas una mejor comprensión de las integrales exponenciales. Si tienes alguna pregunta o quieres compartir tus propias experiencias, ¡no dudes en dejar un comentario!
