Introducción: ¿Por qué es importante entender el volumen y la superficie?
¡Hola a todos! Soy Leandro y hoy vamos a adentrarnos en el fascinante mundo del volumen y la superficie de cuerpos geométricos. Durante mi carrera como ingeniero y docente, he visto cómo estos conceptos pueden parecer complicados al principio, pero con un poco de práctica y comprensión, se vuelven mucho más manejables.
Entender el volumen y la superficie de los cuerpos geométricos es esencial, no solo para los estudiantes de matemáticas y ciencias, sino también para profesionales en ingeniería, arquitectura y muchas otras disciplinas. Estas medidas nos ayudan a describir y entender la forma y el tamaño de los objetos a nuestro alrededor.
Definición de volumen y superficie en cuerpos geométricos
¿Qué es el volumen?
El volumen es una medida del espacio tridimensional que ocupa un objeto. Imagina que tienes una caja y la llenas con agua. El volumen sería la cantidad de agua que cabe dentro de esa caja.
El volumen se mide en unidades cúbicas, como metros cúbicos (m³), centímetros cúbicos (cm³), litros, entre otros. Es crucial para entender cómo interactúan los objetos en un espacio tridimensional.
¿Qué es la superficie?
La superficie, por otro lado, es la medida del área total que cubre un objeto. En términos sencillos, es la «piel» del objeto. Si envolvieras un objeto con papel de regalo, la cantidad de papel que necesitarías sería su superficie.
La superficie se mide en unidades cuadradas, como metros cuadrados (m²), centímetros cuadrados (cm²), entre otros. Conocer la superficie es vital para tareas que van desde la pintura de una pared hasta la fabricación de envolturas.
Fórmulas esenciales para calcular el volumen y la superficie
Volumen de cuerpos geométricos comunes
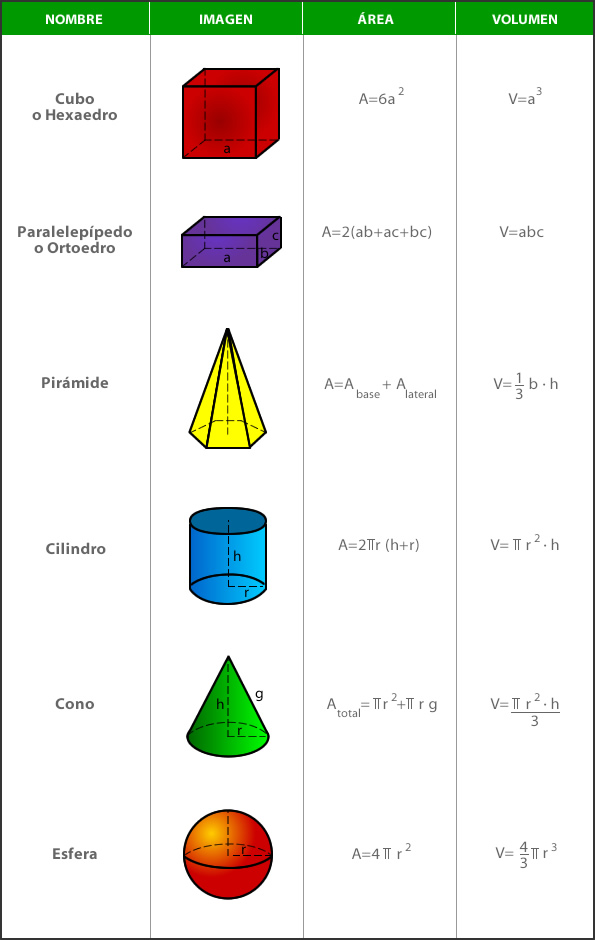
Existen varias fórmulas para calcular el volumen de diferentes cuerpos geométricos. A continuación, te presento algunas de las más comunes:
Volumen de un cubo
La fórmula para el volumen de un cubo es V = a³, donde «a» es la longitud de una arista del cubo.
Volumen de un prisma rectangular
La fórmula para el volumen de un prisma rectangular es V = l × w × h, donde «l» es la longitud, «w» es el ancho y «h» es la altura.
Volumen de una esfera
La fórmula para el volumen de una esfera es V = (4/3)πr³, donde «r» es el radio de la esfera.
Volumen de un cilindro
La fórmula para el volumen de un cilindro es V = πr²h, donde «r» es el radio de la base y «h» es la altura.
Volumen de un cono
La fórmula para el volumen de un cono es V = (1/3)πr²h, donde «r» es el radio de la base y «h» es la altura.
Superficie de cuerpos geométricos comunes
Al igual que con el volumen, existen varias fórmulas para calcular la superficie de diferentes cuerpos geométricos. Aquí tienes algunas de las más comunes:
Superficie de un cubo
La fórmula para la superficie de un cubo es S = 6a², donde «a» es la longitud de una arista del cubo.
Superficie de un prisma rectangular
La fórmula para la superficie de un prisma rectangular es S = 2lw + 2lh + 2wh, donde «l» es la longitud, «w» es el ancho y «h» es la altura.
Superficie de una esfera
La fórmula para la superficie de una esfera es S = 4πr², donde «r» es el radio de la esfera.
Superficie de un cilindro
La fórmula para la superficie de un cilindro es S = 2πrh + 2πr², donde «r» es el radio de la base y «h» es la altura.
Superficie de un cono
La fórmula para la superficie de un cono es S = πr(r + l), donde «r» es el radio de la base y «l» es la longitud de la generatriz.
Aplicaciones prácticas del cálculo de volumen y superficie
Conocer cómo calcular el volumen y la superficie de cuerpos geométricos tiene muchas aplicaciones prácticas en la vida diaria y en diversas profesiones. Aquí te dejo algunos ejemplos:
En la construcción y arquitectura
Los arquitectos y constructores utilizan estos cálculos para diseñar edificios y estructuras. Saber el volumen y la superficie de los materiales les ayuda a estimar costos y cantidades de manera eficiente.
En la ingeniería
Los ingenieros aplican estos conceptos para diseñar y analizar componentes mecánicos, estructuras y sistemas. Desde el diseño de un puente hasta la fabricación de piezas de maquinaria, el volumen y la superficie son fundamentales.
En la vida cotidiana
Incluso en tareas simples como pintar una habitación o llenar una piscina, estos cálculos nos ayudan a estimar la cantidad de pintura o agua necesaria, evitando así gastos innecesarios.
Cómo elegir entre volumen y superficie: ¿Cuál es más importante?
La importancia de conocer el volumen o la superficie depende del contexto y del problema que estés tratando de resolver. Aquí te dejo algunos casos para ayudarte a decidir cuál es más relevante:
Cuando el volumen es más importante
El volumen es crucial cuando necesitas saber la capacidad de un objeto. Por ejemplo, si estás diseñando un tanque de agua, lo más importante es cuánto líquido puede contener. En este caso, el volumen es la medida clave.
Cuando la superficie es más importante
La superficie es más relevante cuando necesitas saber cuánta área externa tiene un objeto. Por ejemplo, si estás pintando una pared, lo que te interesa es la cantidad de área que necesitas cubrir con pintura. Aquí, la superficie es la medida que debes considerar.
Recursos adicionales y enlaces recomendados
Para aquellos que quieran profundizar más en estos conceptos, aquí dejo algunos recursos adicionales y enlaces útiles:
