Triángulos // Geometría
Introducción a los Triángulos en Geometría
Hola, soy Leandro, y hoy vamos a sumergirnos en el fascinante mundo de los triángulos en la geometría. A lo largo de mi vida, he tenido la oportunidad de estudiar, enseñar y aplicar la geometría de maneras que nunca imaginé cuando empecé. Los triángulos, en particular, son figuras que tienen una magia especial. Son simples pero complejos, y se encuentran por todas partes en nuestro mundo. Así que, ¿por qué no explorarlos juntos?
¿Qué es un Triángulo?
Un triángulo es una figura geométrica que tiene tres lados, tres vértices y tres ángulos. Es una de las formas más básicas y fundamentales en la geometría. Los triángulos no solo son interesantes desde un punto de vista matemático, sino que también tienen aplicaciones prácticas en la ingeniería, la arquitectura y muchas otras disciplinas.
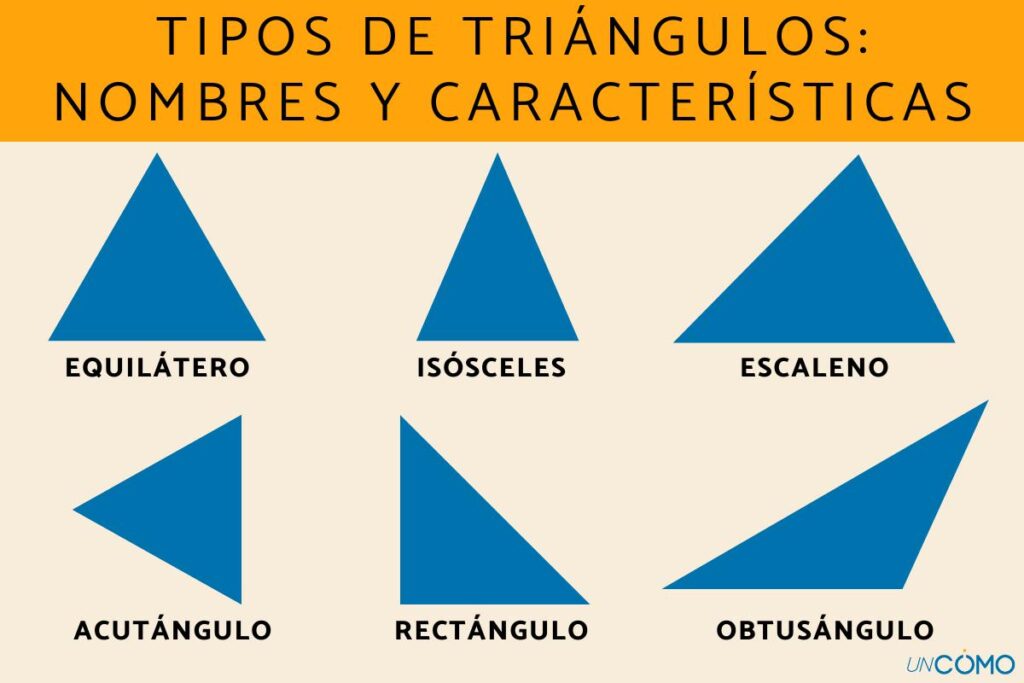
Tipos de Triángulos
Triángulos Equiláteros
Un triángulo equilátero es aquel en el que los tres lados tienen la misma longitud y, por lo tanto, los tres ángulos son iguales, cada uno de 60 grados. Este tipo de triángulo es el epítome de la simetría y la perfección en la geometría.
Triángulos Isósceles
Un triángulo isósceles tiene dos lados de igual longitud y un tercer lado diferente. Los dos ángulos opuestos a los lados iguales también son iguales. Este tipo de triángulo es bastante común y presenta una simetría parcial que lo hace interesante de estudiar.
Triángulos Escalenos
Un triángulo escaleno es aquel en el que todos sus lados y ángulos son diferentes entre sí. Aunque pueden parecer menos «perfectos» que los triángulos equiláteros o isósceles, los triángulos escalenos tienen su propio encanto y son igualmente importantes en la geometría.
Propiedades de los Triángulos en Geometría
Los triángulos tienen varias propiedades interesantes que los hacen únicos en la geometría. Algunas de las propiedades más notables incluyen:
- Suma de Ángulos: La suma de los ángulos internos de un triángulo siempre es 180 grados.
- Desigualdad Triangular: La suma de las longitudes de dos lados cualesquiera de un triángulo siempre es mayor que la longitud del tercer lado.
- Área: El área de un triángulo se puede calcular de varias maneras, siendo las más comunes la fórmula de base por altura dividida por dos y la fórmula de Herón.
Aplicaciones Prácticas de los Triángulos
Los triángulos no solo son figuras interesantes para estudiar en la teoría, sino que también tienen muchas aplicaciones prácticas. Aquí hay algunos ejemplos:
- Ingeniería Civil: Los triángulos se utilizan en la construcción de puentes y estructuras debido a su estabilidad y resistencia.
- Diseño Gráfico: Los diseñadores gráficos a menudo utilizan triángulos para crear composiciones equilibradas y visualmente atractivas.
- Astronomía: Los triángulos se utilizan en la triangulación para determinar la distancia de objetos celestes.
Comparación entre Diferentes Tipos de Triángulos
Es importante entender las diferencias entre los distintos tipos de triángulos para saber cuál es el más adecuado para una aplicación específica. Aquí hay una comparación rápida:
| Tipo de Triángulo | Propiedades | Aplicaciones Comunes |
|---|---|---|
| Equilátero | Todos los lados y ángulos son iguales | Simetría perfecta, diseño gráfico, decoración |
| Isósceles | Dos lados y dos ángulos son iguales | Ingeniería, arquitectura, diseño estructural |
| Escaleno | Todos los lados y ángulos son diferentes | Aplicaciones generales, triangulación en topografía |
Recursos y Enlaces Relacionados
Para aquellos que quieran profundizar más en el estudio de los triángulos y la geometría, aquí hay algunos recursos útiles:
Conclusión
Los triángulos son una parte fundamental de la geometría y tienen aplicaciones prácticas en una variedad de campos. Desde la ingeniería hasta el diseño gráfico, los triángulos son esenciales para comprender y aplicar conceptos geométricos. Espero que este artículo haya sido útil para entender mejor qué son los triángulos y por qué son tan importantes. ¡Hasta la próxima!
