Introducción a los Teoremas de Congruencia y Semejanza
¡Hola! Soy Leandro y hoy vamos a sumergirnos en el fascinante mundo de los teoremas de congruencia y semejanza. Estos conceptos son fundamentales en la geometría y son herramientas poderosas para resolver problemas y entender mejor las figuras geométricas. A lo largo de este artículo, te explicaré de manera sencilla y con un tono desenfadado, pero con la autoridad que brinda la experiencia, todo lo que necesitas saber sobre estos teoremas.
¿Qué son los Teoremas de Congruencia?
Empecemos por lo básico: ¿qué rayos son los teoremas de congruencia? Bueno, en términos simples, la congruencia en geometría significa que dos figuras tienen la misma forma y tamaño. Los teoremas de congruencia son reglas que nos permiten determinar si dos figuras son congruentes sin tener que medir cada uno de sus lados y ángulos.
Teorema Lado-Lado-Lado (LLL)
El teorema Lado-Lado-Lado, también conocido como teorema LLL, establece que si los tres lados de un triángulo son congruentes con los tres lados de otro triángulo, entonces los dos triángulos son congruentes. En otras palabras, si coinciden todos los lados, ¡los triángulos son gemelos!
Teorema Lado-Ángulo-Lado (LAL)
Pasemos al teorema Lado-Ángulo-Lado. Este teorema dice que si dos lados y el ángulo comprendido entre ellos en un triángulo son congruentes con dos lados y el ángulo comprendido entre ellos en otro triángulo, entonces los triángulos son congruentes. Es como decir que si tienes dos lados y el ángulo que los une igualitos en ambos triángulos, estos son idénticos.
Teorema Ángulo-Lado-Ángulo (ALA)
El teorema Ángulo-Lado-Ángulo establece que si dos ángulos y el lado comprendido entre ellos en un triángulo son congruentes con dos ángulos y el lado comprendido entre ellos en otro triángulo, entonces los triángulos son congruentes. Es decir, si coinciden dos ángulos y el lado que los une, ¡bingo! Los triángulos son iguales.
¿Qué son los Teoremas de Semejanza?
Ahora que ya dominamos la congruencia, pasemos a los teoremas de semejanza. La semejanza en geometría significa que dos figuras tienen la misma forma, pero no necesariamente el mismo tamaño. Los teoremas de semejanza nos ayudan a determinar si dos figuras son semejantes sin necesidad de medir todas sus partes.
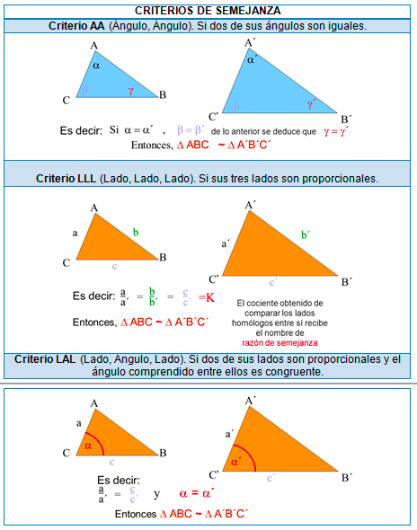
Teorema Ángulo-Ángulo (AA)
El teorema Ángulo-Ángulo es uno de los más simples y útiles. Establece que si dos ángulos de un triángulo son congruentes con dos ángulos de otro triángulo, entonces los triángulos son semejantes. Es como decir que si dos ángulos coinciden, la forma es la misma, aunque el tamaño puede variar.
Teorema Lado-Ángulo-Lado (LAL)
El teorema Lado-Ángulo-Lado para semejanza dice que si dos lados de un triángulo son proporcionales a dos lados de otro triángulo y los ángulos comprendidos son congruentes, entonces los triángulos son semejantes. Aquí, la clave es la proporcionalidad de los lados y la igualdad del ángulo.
Teorema Lado-Lado-Lado (LLL)
Finalmente, el teorema Lado-Lado-Lado para semejanza establece que si los tres lados de un triángulo son proporcionales a los tres lados de otro triángulo, entonces los triángulos son semejantes. Es como decir que si todos los lados están en la misma proporción, la forma es la misma.
Diferencia entre Congruencia y Semejanza
En este punto, ya debes tener una buena idea de qué son los teoremas de congruencia y semejanza, pero quizás te estés preguntando cuál es la diferencia clave entre ellos. La diferencia fundamental radica en que la congruencia implica igualdad de forma y tamaño, mientras que la semejanza implica igualdad de forma pero no necesariamente de tamaño.
Cuándo Usar Congruencia
Usamos los teoremas de congruencia cuando necesitamos probar que dos figuras son idénticas en todos los aspectos. Esto es especialmente útil en problemas de construcción y diseño donde la precisión es crucial.
Cuándo Usar Semejanza
Usamos los teoremas de semejanza cuando queremos demostrar que dos figuras tienen la misma forma, aunque sus tamaños pueden variar. Esto es útil en problemas de escalado y en situaciones donde la forma es más importante que el tamaño exacto.
Aplicaciones de los Teoremas de Congruencia y Semejanza
Los teoremas de congruencia y semejanza no son solo teoría; tienen aplicaciones prácticas en el mundo real. Desde la arquitectura hasta la ingeniería, estos teoremas son herramientas esenciales.
En la Arquitectura
En arquitectura, la congruencia se utiliza para garantizar que las piezas de construcción encajen perfectamente, mientras que la semejanza puede ser útil para crear modelos a escala de edificios.
En la Ingeniería
En ingeniería, la congruencia es crucial para la fabricación de piezas que deben encajar con precisión, mientras que la semejanza se utiliza en el diseño de prototipos y escalado de modelos.
En la Educación
En la educación, entender la congruencia y la semejanza es fundamental para resolver problemas geométricos y para desarrollar habilidades de pensamiento lógico y analítico.
Competencia en el Nicho de Teoremas de Congruencia y Semejanza
Al investigar sobre los teoremas de congruencia y semejanza, encontré que hay varios artículos y blogs que abordan estos temas, pero pocos lo hacen de manera accesible y con un tono desenfadado. Algunos de los sitios más destacados incluyen:
Estos sitios ofrecen explicaciones detalladas y recursos adicionales que pueden complementar lo que has aprendido aquí.
Conclusión
Espero que este artículo te haya ayudado a entender mejor los teoremas de congruencia y semejanza. Estos teoremas son herramientas poderosas en geometría y tienen aplicaciones prácticas en el mundo real. Recuerda, la clave está en saber cuándo usar cada uno y cómo aplicarlos correctamente. Si tienes alguna pregunta o quieres profundizar más en el tema, no dudes en consultar los enlaces que he proporcionado o en buscar más información en línea.
¡Hasta la próxima, y feliz geometría!
