Geometría del Espacio: Una Mirada Profunda
¡Hola! Soy Leandro, un apasionado de las matemáticas y en especial de la geometría. Hoy quiero compartir contigo mis conocimientos sobre un tema fascinante: la Geometría del Espacio. A lo largo de este artículo, desglosaré en qué consiste, sus aplicaciones y cómo se diferencia de la geometría plana. Así que, siéntate, relájate y acompáñame en este viaje tridimensional.
¿Qué es la Geometría del Espacio?
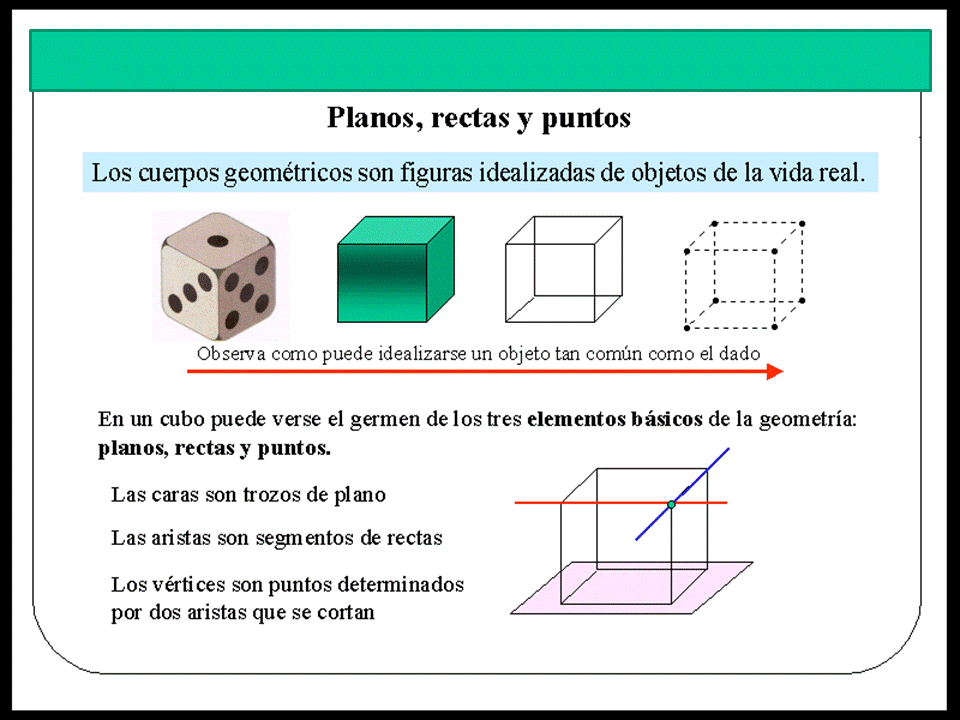
La Geometría del Espacio, también conocida como Geometría Tridimensional o Geometría Espacial, es una rama de las matemáticas que estudia las figuras en tres dimensiones. A diferencia de la geometría plana, que se centra en figuras bidimensionales como triángulos y círculos, la geometría del espacio aborda objetos como cubos, esferas, cilindros y prismas.
Fundamentos de la Geometría del Espacio
Para entender la geometría del espacio, es esencial conocer algunos conceptos básicos:
- Puntos: Los puntos en el espacio se representan mediante coordenadas tridimensionales (x, y, z).
- Líneas: Una línea en el espacio se define por dos puntos y tiene una dirección específica.
- Planos: Un plano es una superficie bidimensional que se extiende infinitamente en todas direcciones dentro del espacio tridimensional.
- Figuras geométricas: Incluyen sólidos como cubos, pirámides, cilindros y esferas.
Aplicaciones de la Geometría del Espacio
La Geometría del Espacio tiene múltiples aplicaciones en diversas áreas. Aquí te presento algunas de las más destacadas:
Arquitectura y Construcción
En arquitectura, la geometría del espacio es fundamental para diseñar estructuras tridimensionales. Desde rascacielos hasta puentes, los arquitectos utilizan principios geométricos para asegurarse de que sus diseños sean estéticamente agradables y estructuralmente sólidos.
Ingeniería
Los ingenieros, especialmente los mecánicos y civiles, emplean la geometría del espacio para desarrollar y analizar sistemas y estructuras. Por ejemplo, en la construcción de maquinaria compleja o en el diseño de infraestructuras como carreteras y túneles.
Robótica y Simulación
En la robótica, la geometría del espacio es crucial para la navegación y la manipulación de objetos en un entorno tridimensional. Los robots deben calcular trayectorias y posiciones precisas para realizar tareas específicas.
Arte y Diseño
Los artistas y diseñadores utilizan la geometría del espacio para crear obras tridimensionales impresionantes. Esculturas, instalaciones artísticas y diseño de interiores son solo algunas de las áreas donde la geometría espacial juega un papel importante.
Diferencias entre la Geometría del Espacio y la Geometría Plana
Aunque ambas ramas de la geometría comparten principios básicos, existen diferencias clave:
Dimensiones
La Geometría Plana se ocupa de figuras en dos dimensiones (ancho y alto), mientras que la Geometría del Espacio abarca tres dimensiones (ancho, alto y profundidad).
Figuras Geométricas
En la geometría plana, trabajamos con figuras como triángulos, cuadrados y círculos. En la geometría del espacio, las figuras incluyen cubos, esferas, cilindros y prismas.
Aplicaciones
Las aplicaciones de la geometría plana suelen estar relacionadas con el diseño gráfico, la cartografía y la creación de planos. Por otro lado, la geometría del espacio se aplica en áreas que requieren un análisis tridimensional, como la arquitectura, la ingeniería y la robótica.
Recursos Relacionados
Si deseas profundizar más en el tema de la geometría del espacio, te recomiendo visitar los siguientes enlaces:
Explorando la Competencia
Para ofrecerte el mejor contenido, he investigado algunos sitios que también abordan el tema de la geometría del espacio. Estos son algunos de los más relevantes:
- Matemáticas Visuales: Un sitio excelente que utiliza visualizaciones para explicar conceptos matemáticos complejos.
- GeoGebra: Una herramienta interactiva que permite explorar la geometría en todas sus formas.
- Universo Fórmulas: Ofrece una amplia gama de fórmulas y explicaciones sobre geometría.
Conclusión
La Geometría del Espacio es una disciplina fascinante que nos permite entender y explorar el mundo tridimensional que nos rodea. Desde aplicaciones prácticas en arquitectura e ingeniería hasta su uso en el arte y el diseño, sus principios son fundamentales en nuestra vida diaria. Espero que este artículo te haya proporcionado una visión clara y completa sobre el tema. ¡Gracias por acompañarme en este viaje geométrico!
Si tienes alguna pregunta o comentario, no dudes en dejarlo abajo. ¡Estoy aquí para ayudarte!
