¡Hola! Soy Leandro y hoy quiero hablarte de un tema que me apasiona: la Geometría Analítica. Si alguna vez has tenido curiosidad por saber de qué trata exactamente o cómo se diferencia de otras ramas de la matemática, estás en el lugar correcto. A lo largo de este artículo, te llevaré de la mano para que entiendas todo lo que necesitas saber sobre este fascinante campo.
¿Qué es la Geometría Analítica?
La Geometría Analítica es una rama de las matemáticas que utiliza el álgebra y el análisis matemático para estudiar y representar figuras geométricas. A diferencia de la geometría clásica, que se basa en construcciones y demostraciones con reglas y compases, la geometría analítica se apoya en el sistema de coordenadas cartesianas para describir las propiedades y relaciones de las figuras.
En términos más sencillos, la geometría analítica nos permite transformar problemas geométricos en ecuaciones algebraicas y, a partir de ahí, resolverlos utilizando técnicas algebraicas. Esto abre un abanico de posibilidades para el análisis y la solución de problemas que, de otra forma, serían mucho más complejos de abordar.
Historia de la Geometría Analítica
La historia de la Geometría Analítica tiene sus raíces en el siglo XVII. Fue desarrollada principalmente por René Descartes y Pierre de Fermat. Descartes, en su obra «La Geometría», introdujo el concepto de coordenadas cartesianas, mientras que Fermat trabajó en paralelo en muchos de los mismos conceptos, aunque su enfoque fue ligeramente diferente.
El trabajo de estos dos matemáticos sentó las bases para una nueva forma de entender y trabajar con la geometría, integrando el álgebra y permitiendo un enfoque más flexible y poderoso para la resolución de problemas.
Conceptos Claves en la Geometría Analítica
Coordenadas Cartesianas
El sistema de coordenadas cartesianas es fundamental en la geometría analítica. Este sistema utiliza dos ejes perpendiculares, generalmente denominados eje X (horizontal) y eje Y (vertical), para definir la posición de un punto en el plano. Cada punto se representa mediante un par de números (x, y) que indican su posición respecto a estos ejes.
Ecuaciones de la Recta
Una de las aplicaciones más comunes de la geometría analítica es la representación de rectas mediante ecuaciones. La forma más básica es la ecuación lineal, que se expresa como y = mx + b, donde m es la pendiente de la recta y b es la intersección con el eje Y.
Además de esta forma, existen otras representaciones como la forma punto-pendiente, la forma general y la forma simétrica, cada una con sus propias ventajas y aplicaciones.
Secciones Cónicas
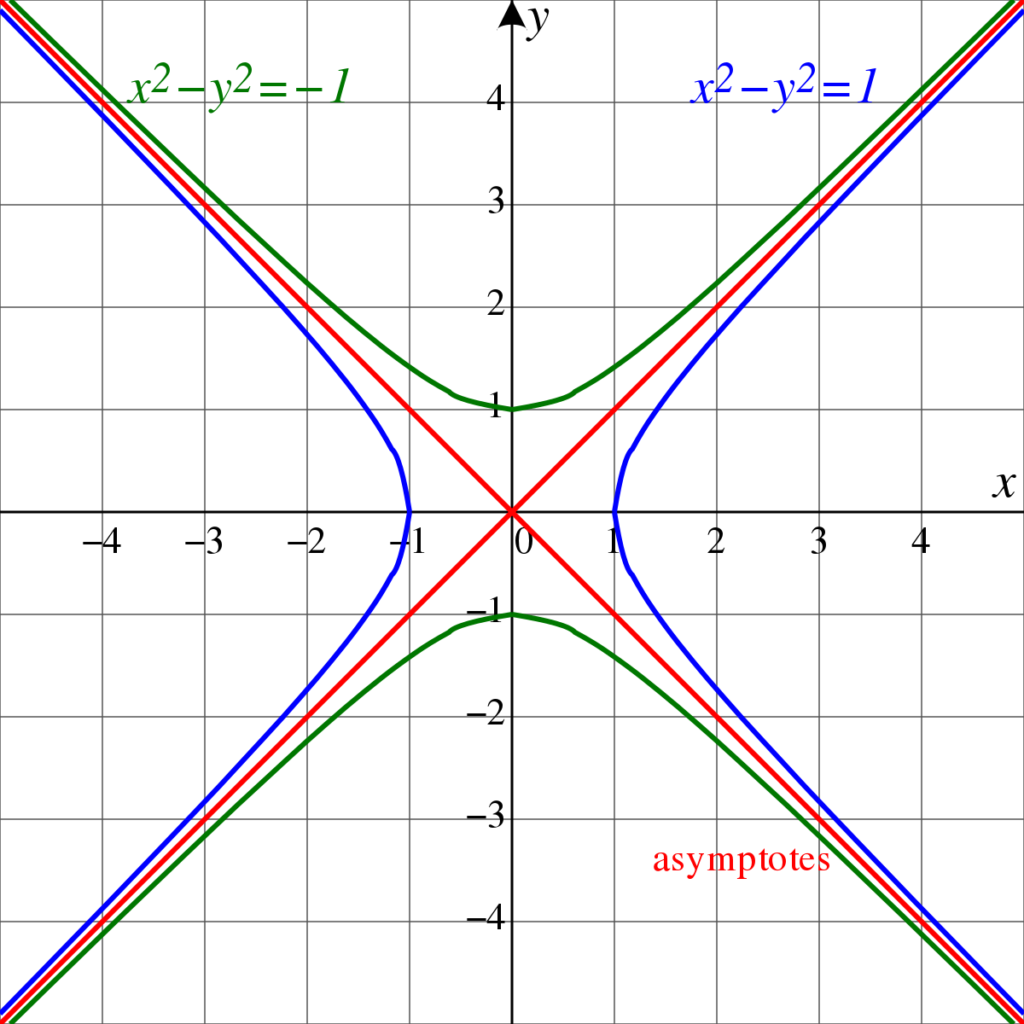
Las secciones cónicas son figuras geométricas que se obtienen al cortar un cono con un plano. Las principales secciones cónicas son la elipse, la parábola y la hipérbola. Cada una de estas figuras tiene su propia ecuación algebraica que describe su forma y propiedades.
La geometría analítica nos permite estudiar estas figuras en detalle, analizando sus características y propiedades a través de sus ecuaciones.
Aplicaciones de la Geometría Analítica
La geometría analítica tiene una amplia gama de aplicaciones en diversas áreas de la ciencia y la ingeniería. Aquí te menciono algunas de las más destacadas:
Física
En física, la geometría analítica se utiliza para describir y analizar movimientos y fuerzas. Por ejemplo, el estudio de trayectorias de objetos en movimiento, como la trayectoria de un proyectil, se puede abordar utilizando ecuaciones de parábolas.
Además, las leyes del movimiento de Newton y otras leyes físicas fundamentales se pueden expresar y analizar mediante ecuaciones algebraicas en un sistema de coordenadas.
Ingeniería
En ingeniería, la geometría analítica es esencial para el diseño y análisis de estructuras y sistemas. Desde la planificación de edificios y puentes hasta el diseño de circuitos eléctricos, la capacidad de representar y resolver problemas geométricos mediante ecuaciones algebraicas es una herramienta invaluable.
Computación Gráfica
En el campo de la computación gráfica, la geometría analítica juega un papel crucial en la representación y manipulación de imágenes y objetos en 3D. Los algoritmos de renderizado y transformación de imágenes utilizan conceptos de geometría analítica para crear efectos visuales realistas y precisos.
Geometría Analítica vs Geometría Euclidiana
Una pregunta común que suele surgir es: ¿Cuál es la diferencia entre la geometría analítica y la geometría euclidiana? La respuesta radica en el enfoque y las herramientas utilizadas en cada una.
La geometría euclidiana, también conocida como geometría clásica, se basa en axiomas y postulados formulados por Euclides en su obra «Los Elementos». Esta rama de la geometría se centra en construcciones y demostraciones utilizando reglas, compases y otros instrumentos geométricos.
Por otro lado, la geometría analítica, como hemos visto, utiliza el álgebra y el sistema de coordenadas para estudiar y representar figuras geométricas. Esta integración del álgebra permite abordar problemas más complejos y realizar análisis más detallados que los posibles con la geometría euclidiana.
Recursos Adicionales y Enlaces Relacionados
Si deseas profundizar más en el estudio de la geometría analítica, te recomiendo revisar los siguientes recursos:
- Wikipedia – Geometría Analítica
- Khan Academy – Analytic Geometry
- GeoGebra – Recursos de Geometría Analítica
Conclusión
La geometría analítica es una rama fascinante de las matemáticas que nos permite abordar problemas geométricos de manera más flexible y poderosa mediante el uso del álgebra y el sistema de coordenadas. Desde sus raíces históricas con René Descartes y Pierre de Fermat hasta sus aplicaciones modernas en física, ingeniería y computación gráfica, la geometría analítica sigue siendo una herramienta esencial en el arsenal de cualquier matemático o científico.
Espero que este artículo te haya dado una visión clara y completa de lo que es la geometría analítica y cómo se diferencia de otras ramas de la geometría. Si tienes alguna pregunta o comentario, no dudes en dejarlo a continuación. ¡Hasta la próxima!
