Geometría Algebraica: Una Introducción Completa
¿Qué es la Geometría Algebraica?
¡Hola! Soy Leandro, y hoy quiero hablarte sobre uno de mis temas favoritos: la Geometría Algebraica. Este campo fascinante de las matemáticas combina dos áreas que pueden parecer muy diferentes a primera vista: la geometría y el álgebra.
En términos sencillos, la Geometría Algebraica es la rama de las matemáticas que estudia las soluciones de sistemas de ecuaciones algebraicas. Es decir, se encarga de analizar las propiedades geométricas de los conjuntos de puntos que satisfacen dichas ecuaciones.
Fundamentos de la Geometría Algebraica
Para entender mejor la Geometría Algebraica, es esencial conocer algunos conceptos básicos. Aquí te dejo una breve introducción:
Variedades Algebraicas
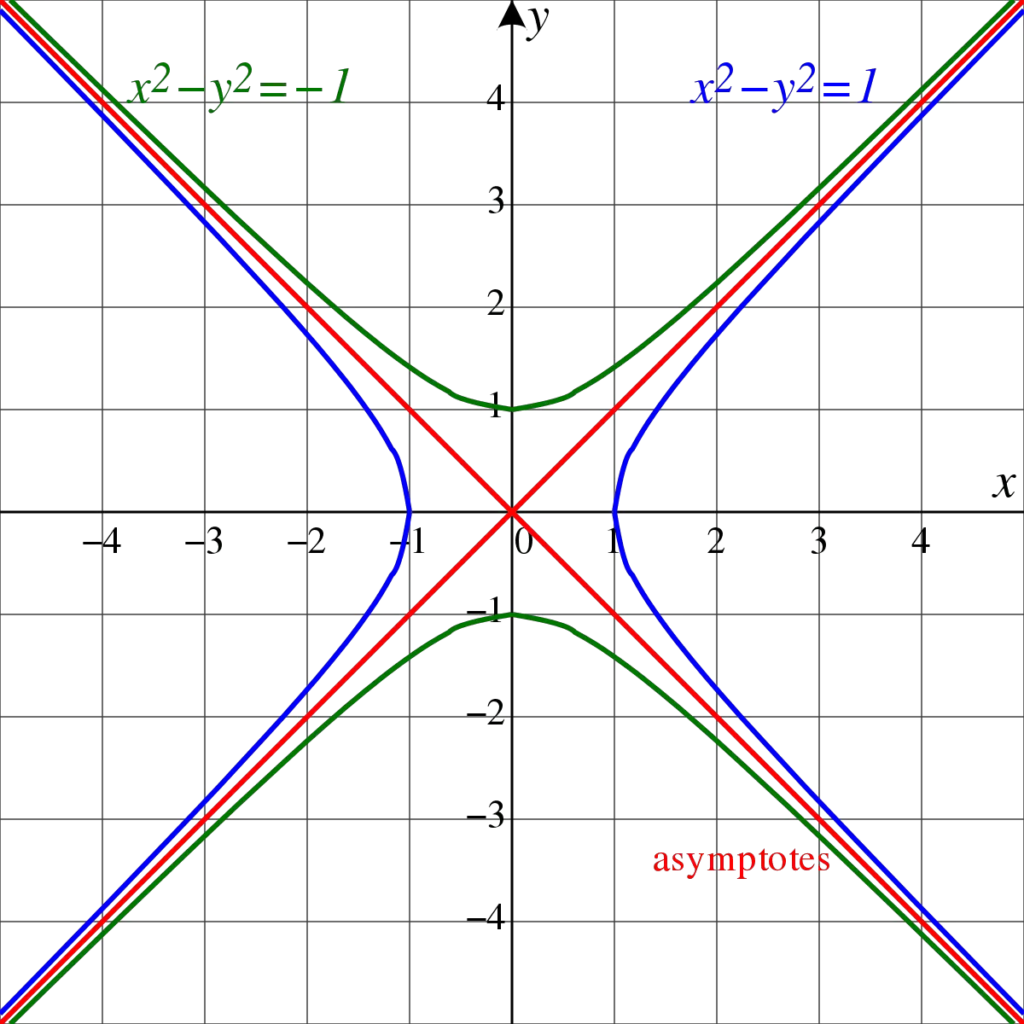
Uno de los conceptos centrales en Geometría Algebraica es el de variedad algebraica. Una variedad algebraica es el conjunto de soluciones de un sistema de ecuaciones polinómicas. Por ejemplo, una circunferencia en el plano puede describirse con la ecuación x2 + y2 = r2.
Mapas y Morfismos
Otro concepto clave son los mapas o morfismos entre variedades algebraicas. Estos son funciones que preservan la estructura algebraica de las variedades. En otras palabras, permiten «traducir» propiedades de una variedad a otra.
Herramientas y Técnicas
La Geometría Algebraica utiliza una variedad de herramientas matemáticas, incluyendo la teoría de anillos, la teoría de módulos y la topología algebraica. Estas herramientas permiten a los matemáticos trabajar con objetos geométricos utilizando métodos algebraicos.
Aplicaciones de la Geometría Algebraica
La Geometría Algebraica no es solo una teoría abstracta; tiene muchas aplicaciones prácticas en diversas áreas. Aquí te dejo algunas de las más interesantes:
Criptografía
En criptografía, la Geometría Algebraica juega un papel crucial. Los códigos algebraicos se utilizan para encriptar información de manera segura. Un ejemplo famoso es el criptosistema de curvas elípticas, que se basa en propiedades de las variedades algebraicas.
Teoría de Números
La Geometría Algebraica también tiene aplicaciones en la Teoría de Números. Por ejemplo, el famoso último teorema de Fermat fue finalmente demostrado utilizando técnicas de Geometría Algebraica.
Física Teórica
En física teórica, especialmente en la teoría de cuerdas, la Geometría Algebraica es una herramienta fundamental. Las variedades algebraicas se utilizan para describir las formas complejas de los espacios que aparecen en estas teorías.
Diferencias entre Geometría Algebraica y Otras Ramas Matemáticas
Es común que las personas se confundan entre la Geometría Algebraica y otras ramas de las matemáticas. A continuación, te explico algunas diferencias clave:
Geometría Algebraica vs. Geometría Diferencial
La Geometría Diferencial se centra en el estudio de curvas y superficies utilizando el cálculo diferencial e integral. En cambio, la Geometría Algebraica utiliza métodos algebraicos y estudia conjuntos de soluciones de ecuaciones polinómicas.
Geometría Algebraica vs. Álgebra Abstracta
El Álgebra Abstracta se ocupa del estudio de estructuras algebraicas como grupos, anillos y campos. Aunque la Geometría Algebraica también utiliza estas estructuras, su enfoque principal es el estudio geométrico de las soluciones de ecuaciones algebraicas.
Geometría Algebraica vs. Topología
La Topología estudia las propiedades de los espacios que permanecen invariantes bajo deformaciones continuas. La Geometría Algebraica, por otro lado, se enfoca en las propiedades algebraicas de los conjuntos de soluciones de ecuaciones polinómicas.
Recursos y Enlaces Recomendados
Si quieres profundizar en la Geometría Algebraica, aquí te dejo algunos recursos y enlaces recomendados:
Conclusión
La Geometría Algebraica es una disciplina matemática rica y fascinante que combina lo mejor de dos mundos: la geometría y el álgebra. Sus aplicaciones prácticas en criptografía, teoría de números y física teórica demuestran su relevancia y utilidad. Espero que este artículo te haya dado una buena introducción a este emocionante campo. ¡Gracias por leer!
