Introducción a las Coordenadas Cartesianas y la Geometría Analítica
¡Hola! Soy Leandro, y hoy vengo a hablarles sobre dos pilares fundamentales en el mundo de las matemáticas: las Coordenadas Cartesianas y la Geometría Analítica. A lo largo de mi carrera, he tenido la oportunidad de explorar y enseñar estos conceptos, y puedo decir con confianza que son esenciales para entender muchas áreas de las matemáticas y la física. Así que, sin más preámbulos, ¡vamos a sumergirnos en este fascinante tema!
¿Qué son las Coordenadas Cartesianas?
Las Coordenadas Cartesianas son un sistema de referencia que nos permite ubicar puntos en un plano de manera precisa. Este sistema fue desarrollado por René Descartes en el siglo XVII, y ha sido una herramienta crucial para la evolución de la geometría y el análisis matemático.
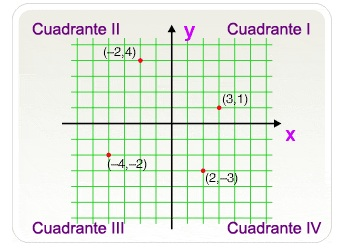
En su forma más básica, un sistema de coordenadas cartesianas consta de dos ejes perpendiculares: el eje X (horizontal) y el eje Y (vertical). Cada punto en el plano puede ser representado por un par de números (x, y), donde ‘x’ es la coordenada en el eje horizontal y ‘y’ es la coordenada en el eje vertical.
¿Qué es la Geometría Analítica?
La Geometría Analítica, por otro lado, es una rama de las matemáticas que utiliza el álgebra para estudiar las propiedades geométricas. Se basa en el uso de las Coordenadas Cartesianas para representar figuras geométricas y resolver problemas relacionados con ellas. Es como si combináramos lo mejor de dos mundos: la precisión del álgebra y la intuición visual de la geometría.
Esta disciplina nos permite analizar y describir figuras como líneas, círculos y parábolas mediante ecuaciones algebraicas. De esta manera, podemos resolver problemas complejos de manera más rápida y eficiente.
Relación entre Coordenadas Cartesianas y Geometría Analítica
Las Coordenadas Cartesianas y la Geometría Analítica están intrínsecamente relacionadas. De hecho, no podríamos tener Geometría Analítica sin un sistema de coordenadas para trabajar. Las coordenadas nos proporcionan la herramienta necesaria para traducir problemas geométricos en ecuaciones algebraicas que podemos manipular y resolver.
Por ejemplo, consideremos la ecuación de una línea recta en un plano cartesiano: y = mx + b. Aquí, ‘m’ representa la pendiente de la línea y ‘b’ es el punto de intersección con el eje Y. Esta simple ecuación nos permite analizar la inclinación y posición de la línea en el plano, todo gracias a las Coordenadas Cartesianas.
Aplicaciones Prácticas de las Coordenadas Cartesianas y la Geometría Analítica
Las aplicaciones de las Coordenadas Cartesianas y la Geometría Analítica son vastas y variadas. En la física, por ejemplo, se utilizan para describir el movimiento de objetos y analizar fuerzas. En la ingeniería, son fundamentales para el diseño y análisis de estructuras y sistemas.
En el mundo de la informática, las gráficas y los videojuegos dependen en gran medida de las coordenadas cartesianas para renderizar imágenes y animaciones. Incluso en la vida cotidiana, utilizamos conceptos de coordenadas cuando usamos mapas y GPS para navegar.
Ejemplo de Aplicación: Trayectorias de Proyectiles
Un ejemplo clásico es el análisis de la trayectoria de un proyectil. Mediante la Geometría Analítica, podemos modelar la trayectoria de un objeto lanzado al aire y predecir su punto de aterrizaje. Utilizando las ecuaciones del movimiento y las Coordenadas Cartesianas, podemos calcular la altura máxima alcanzada, la distancia recorrida y el tiempo de vuelo.
Ejemplo de Aplicación: Diseño Gráfico
En el diseño gráfico y la animación, las Coordenadas Cartesianas son esenciales para posicionar y mover objetos en una pantalla. Por ejemplo, al crear una animación, cada fotograma puede ser representado como un conjunto de puntos con coordenadas específicas, lo que permite una manipulación precisa y coherente de los elementos visuales.
Ventajas y Desventajas de las Coordenadas Cartesianas y la Geometría Analítica
Como todo en la vida, tanto las Coordenadas Cartesianas como la Geometría Analítica tienen sus ventajas y desventajas. Vamos a analizar algunos de estos aspectos.
Ventajas
- Precisión: Las coordenadas cartesianas permiten una representación precisa de puntos y figuras en un plano.
- Facilidad de Uso: Una vez que se comprende el sistema, es relativamente fácil de usar y aplicar a diversos problemas geométricos y algebraicos.
- Versatilidad: La Geometría Analítica puede aplicarse a una amplia gama de problemas en matemáticas, física, ingeniería y más.
Desventajas
- Complejidad: Algunos problemas pueden volverse muy complejos y requerir un alto nivel de habilidad matemática para resolver.
- Limitaciones Dimensionales: Las coordenadas cartesianas tradicionales se limitan a dos dimensiones, aunque existen extensiones tridimensionales.
- Dependencia de la Representación: La precisión y utilidad del sistema dependen de una correcta representación y manipulación de las ecuaciones y coordenadas.
Comparación con Otros Sistemas de Coordenadas
Es importante destacar que las Coordenadas Cartesianas no son el único sistema de coordenadas utilizado en matemáticas y ciencias. Existen otros sistemas, como las coordenadas polares y cilíndricas, cada uno con sus propias ventajas y aplicaciones.
Coordenadas Polares
Las coordenadas polares se utilizan para representar puntos en un plano mediante un ángulo y una distancia desde un punto de origen. Este sistema es especialmente útil para problemas que involucran simetría radial, como el movimiento circular.
Coordenadas Cilíndricas y Esféricas
En tres dimensiones, las coordenadas cilíndricas y esféricas son extensiones de las coordenadas polares. Las coordenadas cilíndricas se utilizan para problemas que tienen simetría alrededor de un eje, mientras que las coordenadas esféricas son útiles para describir posiciones en una esfera.
En comparación, las Coordenadas Cartesianas son más intuitivas y fáciles de entender para la mayoría de las personas, especialmente cuando se trata de problemas en dos dimensiones. Sin embargo, dependiendo del problema específico, otros sistemas de coordenadas pueden ser más apropiados y eficientes.
Recursos Adicionales y Enlaces Relacionados
Para aquellos interesados en profundizar más en el tema de las Coordenadas Cartesianas y la Geometría Analítica, aquí hay algunos recursos adicionales que pueden resultar útiles:
Reflexiones Finales
En resumen, las Coordenadas Cartesianas y la Geometría Analítica son herramientas poderosas y esenciales en el mundo de las matemáticas. Nos permiten entender y resolver problemas complejos de manera precisa y eficiente. Aunque pueden parecer intimidantes al principio, con práctica y estudio, cualquiera puede dominar estos conceptos y aplicarlos en diversas áreas.
Espero que este artículo haya sido útil y que hayan disfrutado aprendiendo sobre este fascinante tema tanto como yo disfruto enseñándolo. Si tienen alguna pregunta o comentario, no duden en dejarlo abajo. ¡Hasta la próxima!
