Geometría
¡Hola! Soy Leandro y hoy vengo a hablaros de un tema fascinante: los ángulos en la geometría. Si alguna vez te has sentado a pensar en la importancia de los ángulos en nuestras vidas, este artículo te abrirá los ojos. Desde la construcción de edificios hasta la creación de gráficos, los ángulos están en todas partes. Acompáñame en este viaje por el maravilloso mundo de los ángulos y la geometría.
¿Qué son los Ángulos?
Primero lo primero, ¿Qué demonios es un ángulo? En términos sencillos, un ángulo se forma cuando dos líneas se cruzan en un punto. Este punto de cruce se llama vértice y las líneas se conocen como lados del ángulo. La medida de un ángulo se da en grados, que van desde 0° hasta 360°.
Si te interesa profundizar más en la definición técnica, te recomiendo este artículo de Wikipedia sobre ángulos.
Tipos de Ángulos en Geometría
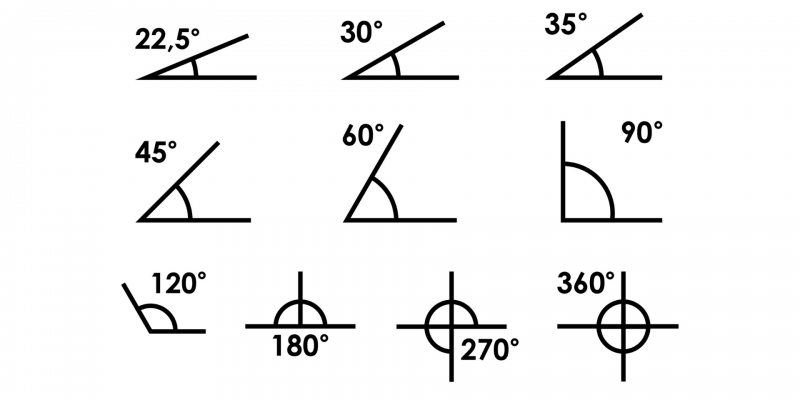
Hay varios tipos de ángulos que se clasifican según su medida. Conocer estos tipos te ayudará a entender mejor cómo funcionan en la práctica.
Ángulo Agudo
Un ángulo agudo es aquel que mide menos de 90°. Estos ángulos son menores y se encuentran comúnmente en figuras como triángulos.
Ángulo Recto
El ángulo recto mide exactamente 90°. Es uno de los ángulos más importantes en geometría, ya que forma la base de muchas construcciones y teorías.
Ángulo Obtuso
Un ángulo obtuso mide entre 90° y 180°. Estos ángulos son más amplios y se pueden encontrar en diversas figuras geométricas.
Ángulo Llano
El ángulo llano mide exactamente 180°. Es una línea recta y se forma cuando dos ángulos rectos se unen.
Ángulo Completo
Un ángulo completo mide 360°. Este ángulo forma un círculo completo y es útil en diversas aplicaciones como la navegación y el diseño gráfico.
Aplicaciones de los Ángulos en la Vida Cotidiana
Ahora que ya sabes qué son los ángulos y sus tipos, vamos a ver cómo se aplican en nuestra vida cotidiana.
Ángulos en la Arquitectura
La arquitectura es un campo donde los ángulos juegan un papel crucial. Desde la construcción de rascacielos hasta el diseño de puentes, los ángulos ayudan a determinar la estabilidad y estética de las estructuras.
Si te interesa saber más sobre la aplicación de ángulos en arquitectura, te recomiendo este artículo de ArchDaily.
Ángulos en el Diseño Gráfico
En el diseño gráfico, los ángulos se utilizan para crear efectos visuales y dar una sensación de profundidad. Los diseñadores usan ángulos para dirigir la atención del espectador y para crear composiciones equilibradas.
Ángulos en la Navegación
Los navegantes y pilotos utilizan ángulos para determinar rutas y trayectorias. Los ángulos de elevación y declinación son esenciales para la navegación precisa.
Cómo Medir Ángulos
Medir ángulos puede parecer complicado, pero con las herramientas adecuadas, es bastante sencillo.
Uso del Transportador
El transportador es una herramienta común para medir ángulos. Consiste en un semicírculo graduado en grados, que te permite medir cualquier ángulo con precisión.
Medición Digital
En la era digital, también puedes utilizar aplicaciones y software para medir ángulos. Estas herramientas son especialmente útiles en campos como el diseño gráfico y la ingeniería.
Ángulos en la Geometría Euclidiana
La geometría euclidiana, desarrollada por el matemático griego Euclides, se basa en la noción de ángulos y líneas rectas. En esta geometría, los ángulos se utilizan para demostrar teoremas y propiedades de figuras geométricas.
Postulados de Euclides
Los postulados de Euclides, también conocidos como axiomas, son las bases de la geometría euclidiana. Uno de los postulados más importantes es que la suma de los ángulos interiores de un triángulo es siempre 180°.
Teorema de Pitágoras
El Teorema de Pitágoras es otro concepto fundamental que utiliza ángulos. Este teorema establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados.
Ángulos en la Geometría No Euclidiana
La geometría no euclidiana es una extensión de la geometría euclidiana que explora conceptos más allá de las líneas rectas y ángulos tradicionales. En esta geometría, los ángulos pueden comportarse de maneras inesperadas.
Geometría Hiperbólica
En la geometría hiperbólica, los ángulos en un triángulo suman menos de 180°. Este tipo de geometría se utiliza en teorías avanzadas de física y matemáticas.
Geometría Esférica
En la geometría esférica, los ángulos en un triángulo suman más de 180°. Esta geometría es útil en la navegación y la astronomía.
Herramientas y Recursos Adicionales
Si deseas profundizar más en el tema de los ángulos y la geometría, aquí tienes algunos recursos adicionales que te pueden ser útiles:
- Khan Academy – Geometría
- Coursera – Introducción a la Geometría
- GeoGebra – Herramientas de Geometría
Conclusión
Espero que este artículo te haya proporcionado una visión completa sobre los ángulos en la geometría. Desde su definición básica hasta sus aplicaciones en la vida cotidiana y las diferencias entre geometría euclidiana y no euclidiana, los ángulos son una parte integral de nuestro mundo. Si tienes alguna pregunta o quieres saber más sobre algún aspecto específico, no dudes en dejar un comentario. ¡Hasta la próxima!
