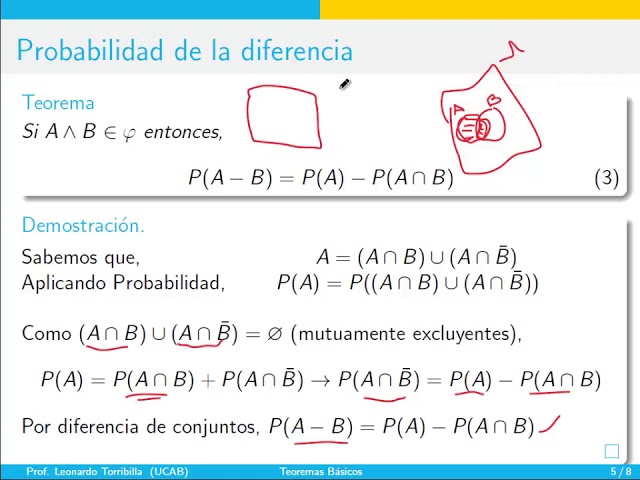
Teoremas de Probabilidad – Guía Completa

¡Hola! Soy Leandro, y hoy vamos a adentrarnos en el fascinante mundo de los teoremas de probabilidad. Este es un tema que puede sonar un poco intimidante, pero te prometo que, con un poco de paciencia, todo comenzará a tener sentido. A lo largo de este artículo, desglosaré los conceptos clave, te mostraré ejemplos prácticos y te ayudaré a entender por qué estos teoremas son cruciales en la teoría de probabilidad.

¿Qué son los Teoremas de Probabilidad?

La probabilidad es una rama de las matemáticas que se ocupa de analizar fenómenos aleatorios. Dentro de este campo, los teoremas de probabilidad son resultados matemáticos que nos permiten calcular y entender mejor la probabilidad de diferentes eventos. Estos teoremas son las herramientas que usamos para desentrañar el comportamiento de procesos aleatorios. ¡Así que, si alguna vez te has preguntado por qué el azar parece tener un patrón, estás en el lugar correcto!

Principales Teoremas de Probabilidad

Existen varios teoremas fundamentales en la teoría de probabilidad. A continuación, veremos algunos de los más importantes y cómo se aplican:

Teorema de Probabilidad Total

El teorema de probabilidad total es uno de los pilares de la teoría de probabilidad. Este teorema nos permite calcular la probabilidad de un evento A, descomponiéndolo en sub-eventos B₁, B₂, …, B_n que forman una partición del espacio muestral.

La fórmula es la siguiente:

P(A) = Σ P(A|B_i) * P(B_i)

Donde:

• P(A) es la probabilidad del evento A.
• P(A|B_i) es la probabilidad del evento A dado que ocurrió B_i.
• P(B_i) es la probabilidad del sub-evento B_i.

Este teorema es sumamente útil cuando tenemos información parcial sobre el evento que nos interesa.

Teorema de Bayes

El teorema de Bayes es quizás uno de los teoremas más fascinantes y útiles en la teoría de probabilidad. Nos permite actualizar la probabilidad de un evento basado en nueva información. La fórmula del teorema de Bayes es la siguiente:

P(A|B) = [P(B|A) * P(A)] / P(B)

Donde:

• P(A|B) es la probabilidad del evento A dado que ocurrió B.
• P(B|A) es la probabilidad del evento B dado que ocurrió A.
• P(A) es la probabilidad del evento A.
• P(B) es la probabilidad del evento B.

Este teorema tiene aplicaciones en una amplia gama de campos, desde la medicina hasta la inteligencia artificial.

Teorema del Límite Central

El teorema del límite central es fundamental en la estadística y la teoría de probabilidad. Este teorema establece que, bajo ciertas condiciones, la suma de un gran número de variables aleatorias independientes y identicamente distribuidas se aproxima a una distribución normal (gaussiana), independientemente de la distribución original de las variables.

Este teorema es crucial porque justifica el uso de la distribución normal en muchas situaciones prácticas, lo que facilita el análisis y la inferencia estadística.

Aplicaciones Prácticas de los Teoremas de Probabilidad

Ahora que hemos cubierto algunos de los teoremas fundamentales, veamos cómo se aplican en la vida real.

Medicina y Diagnóstico

En medicina, el teorema de Bayes se utiliza para actualizar la probabilidad de una enfermedad basándose en nuevos resultados de pruebas. Por ejemplo, si un paciente tiene un resultado positivo en una prueba, el teorema de Bayes puede ayudar a los médicos a calcular la probabilidad de que el paciente realmente tenga la enfermedad.

Seguros y Riesgo

Las compañías de seguros utilizan los teoremas de probabilidad para evaluar riesgos y calcular primas. Por ejemplo, el teorema de probabilidad total puede ayudar a descomponer el riesgo en varios factores, como la edad, el historial de salud y el estilo de vida.

Finanzas y Predicción del Mercado

En el ámbito financiero, los teoremas de probabilidad son esenciales para modelar el comportamiento del mercado y predecir precios de activos. El teorema del límite central justifica el uso de modelos basados en la distribución normal para estimar rendimientos y riesgos.

Comparación de Teoremas de Probabilidad

Es posible que te preguntes cuál de estos teoremas es mejor o más útil. La verdad es que no hay una respuesta única, ya que cada teorema tiene sus propias aplicaciones y ventajas. Sin embargo, aquí hay algunas consideraciones:

• El teorema de probabilidad total es ideal para situaciones donde tenemos información parcial y queremos descomponer un evento en sub-eventos más manejables.
• El teorema de Bayes es extremadamente útil cuando necesitamos actualizar nuestras creencias basándonos en nueva información.
• El teorema del límite central es esencial en la estadística y la teoría de probabilidad para justificar el uso de la distribución normal en muchos contextos prácticos.

Recursos Adicionales y Enlaces Relacionados

Si quieres profundizar más en los teoremas de probabilidad, te recomiendo los siguientes recursos:

• Wikipedia – Teorema de Probabilidad Total
• Wikipedia – Teorema de Bayes
• Wikipedia – Teorema del Límite Central

Conclusión

Espero que este artículo te haya dado una visión clara y comprensible de los teoremas de probabilidad. Estos teoremas son herramientas poderosas que nos permiten entender y modelar el comportamiento de fenómenos aleatorios en una amplia gama de campos. Recuerda, la clave está en practicar y aplicar estos conceptos en situaciones reales para dominar realmente la teoría de probabilidad.

¡Gracias por acompañarme en este viaje a través de los teoremas de probabilidad! Si tienes alguna pregunta o comentario, no dudes en dejarlo abajo. ¡Hasta la próxima!