Probabilidad Básica y Teorema de la Probabilidad Total
¡Hola! Soy Leandro y hoy vamos a sumergirnos en el fascinante mundo de la probabilidad básica y el teorema de la probabilidad total. Acompáñame en este viaje donde desglosaremos estos conceptos y te mostraré cómo puedes dominar estos temas para aplicarlos en tu día a día.
¿Qué es la Probabilidad Básica?
La probabilidad básica es la rama de las matemáticas que se ocupa de estudiar la posibilidad de que ocurra un evento. En términos simples, es la medida de la certeza o incertidumbre sobre la ocurrencia de un evento. Por ejemplo, cuando lanzas una moneda, la probabilidad de que salga cara es del 50%, es decir, hay una posibilidad entre dos de que ocurra.
Definición Formal de Probabilidad
La probabilidad de un evento A se define como el cociente entre el número de casos favorables y el número total de casos posibles. Matemáticamente, se expresa como:
P(A) = Número de casos favorables / Número total de casos posibles
Este concepto es fundamental en diversos campos como la estadística, economía, ingeniería, y muchos otros. Si quieres profundizar más en la definición formal de probabilidad, te recomiendo leer este artículo de Wikipedia sobre probabilidad.
¿Qué es el Teorema de la Probabilidad Total?
El teorema de la probabilidad total es una herramienta poderosa en la teoría de la probabilidad que nos permite calcular la probabilidad de un evento considerando todas las formas en que ese evento puede ocurrir. Este teorema es especialmente útil cuando un evento puede ser descompuesto en una serie de eventos más simples y mutuamente excluyentes.
Definición Formal del Teorema de la Probabilidad Total
El teorema de la probabilidad total se puede expresar de la siguiente manera:
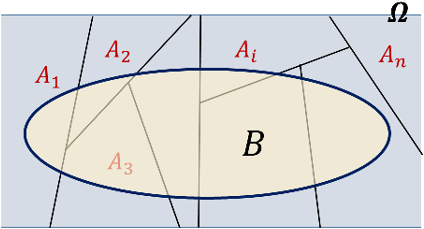
Si {B1, B2, …, Bn} es una partición del espacio muestral S, y A es un evento cualquiera, entonces:
P(A) = P(A ∩ B1) + P(A ∩ B2) + … + P(A ∩ Bn)
O de manera más compacta:
P(A) = Σ P(A | Bi) * P(Bi)
Donde P(A | Bi) es la probabilidad condicional de A dado Bi, y P(Bi) es la probabilidad de Bi. Para explorar más sobre este teorema, te sugiero visitar este enlace de Wikipedia sobre el teorema de la probabilidad total.
Comparación entre Probabilidad Básica y el Teorema de la Probabilidad Total
Ahora que ya tienes una idea clara de lo que son la probabilidad básica y el teorema de la probabilidad total, vamos a compararlos y a entender cuándo usar cada uno.
Probabilidad Básica
La probabilidad básica se utiliza cuando queremos calcular la probabilidad de un solo evento simple o compuesto. Es fundamental para resolver problemas sencillos y es el primer paso en el estudio de la probabilidad.
Teorema de la Probabilidad Total
El teorema de la probabilidad total se utiliza cuando un evento puede ser descompuesto en varios eventos más simples y mutuamente excluyentes. Es una herramienta avanzada que nos permite calcular probabilidades complejas de una manera más estructurada y precisa.
Aplicaciones Prácticas
Veamos algunos ejemplos prácticos donde podemos aplicar estos conceptos para resolver problemas del mundo real.
Ejemplo de Probabilidad Básica
Imagina que tienes una bolsa con 3 bolas rojas y 2 bolas azules. Si sacas una bola al azar, ¿cuál es la probabilidad de que sea roja?
La probabilidad se calcula de la siguiente manera:
P(Roja) = Número de bolas rojas / Número total de bolas = 3/5 = 0.6 o 60%
Ejemplo del Teorema de la Probabilidad Total
Supongamos que tienes tres urnas. La primera tiene 1 bola roja y 3 azules, la segunda tiene 2 bolas rojas y 2 azules, y la tercera tiene 3 bolas rojas y 1 azul. Si eliges una urna al azar y sacas una bola, ¿cuál es la probabilidad de que sea roja?
Podemos usar el teorema de la probabilidad total para resolver este problema. Primero, calculamos la probabilidad de sacar una bola roja de cada urna:
- P(Roja | Urna 1) = 1/4
- P(Roja | Urna 2) = 2/4
- P(Roja | Urna 3) = 3/4
Luego, calculamos la probabilidad de elegir cada urna, que es 1/3 ya que todas tienen la misma probabilidad de ser elegidas:
- P(Urna 1) = 1/3
- P(Urna 2) = 1/3
- P(Urna 3) = 1/3
Usamos el teorema de la probabilidad total para calcular la probabilidad de sacar una bola roja:
P(Roja) = P(Roja | Urna 1) * P(Urna 1) + P(Roja | Urna 2) * P(Urna 2) + P(Roja | Urna 3) * P(Urna 3)
P(Roja) = (1/4 * 1/3) + (2/4 * 1/3) + (3/4 * 1/3)
P(Roja) = 1/12 + 2/12 + 3/12 = 6/12 = 1/2 = 0.5 o 50%
Conclusión
Espero que este artículo te haya ayudado a entender mejor la probabilidad básica y el teorema de la probabilidad total. Ambos conceptos son fundamentales en el estudio de la probabilidad y tienen aplicaciones prácticas en muchos campos. Recuerda que la probabilidad básica es el primer paso para resolver problemas sencillos, mientras que el teorema de la probabilidad total es una herramienta avanzada para calcular probabilidades complejas.
Si quieres profundizar más en estos temas, te recomiendo visitar los siguientes enlaces:
- Khan Academy – Estadística y Probabilidad
- Probabilidad.net
- Coursera – Introduction to Probability and Data
¡Gracias por leer y hasta la próxima!
