Hola, soy Leandro, y hoy quiero hablarte sobre un tema que puede parecer un poco complicado al principio, pero que con un poco de práctica y paciencia, se vuelve una herramienta indispensable: los parámetros estadísticos. A lo largo de mi carrera, he tenido la oportunidad de trabajar con ellos en diversas áreas, y puedo asegurarte que conocerlos bien marcará una gran diferencia en tu análisis de datos.
¿Qué son los Parámetros Estadísticos?
Los parámetros estadísticos son medidas que nos permiten resumir, describir y analizar conjuntos de datos. Son esenciales para entender la distribución y la tendencia de los datos, así como para tomar decisiones informadas basadas en estos. Algunos de los parámetros estadísticos más comunes son la media, la mediana, la moda, la varianza y la desviación estándar.
Media: El Promedio de los Datos
La media, también conocida como promedio, es quizás el parámetro estadístico más conocido. Se calcula sumando todos los valores de un conjunto de datos y dividiéndolos entre el número total de valores. La fórmula matemática es:
Media (μ) = ΣX / N
donde ΣX es la suma de todos los valores y N es el número de valores.
La media es útil porque nos da una idea general del valor central de nuestros datos. Sin embargo, puede ser influenciada por valores atípicos (outliers), por lo que no siempre es la mejor medida de tendencia central.
Mediana: El Valor Central
La mediana es el valor que se encuentra en el centro de un conjunto de datos ordenado. Si el número de valores es impar, la mediana es el valor del medio. Si es par, la mediana es el promedio de los dos valores centrales.
La mediana es una medida robusta de tendencia central porque no se ve afectada por valores atípicos. Es especialmente útil cuando los datos están sesgados o contienen outliers.
Moda: El Valor Más Frecuente
La moda es el valor que aparece con más frecuencia en un conjunto de datos. Un conjunto de datos puede tener una moda, más de una moda (multimodal) o ninguna moda (si todos los valores son únicos).
La moda es útil para entender la frecuencia de ocurrencia de un valor en particular en nuestros datos. Sin embargo, no siempre es representativa del conjunto de datos en su totalidad.
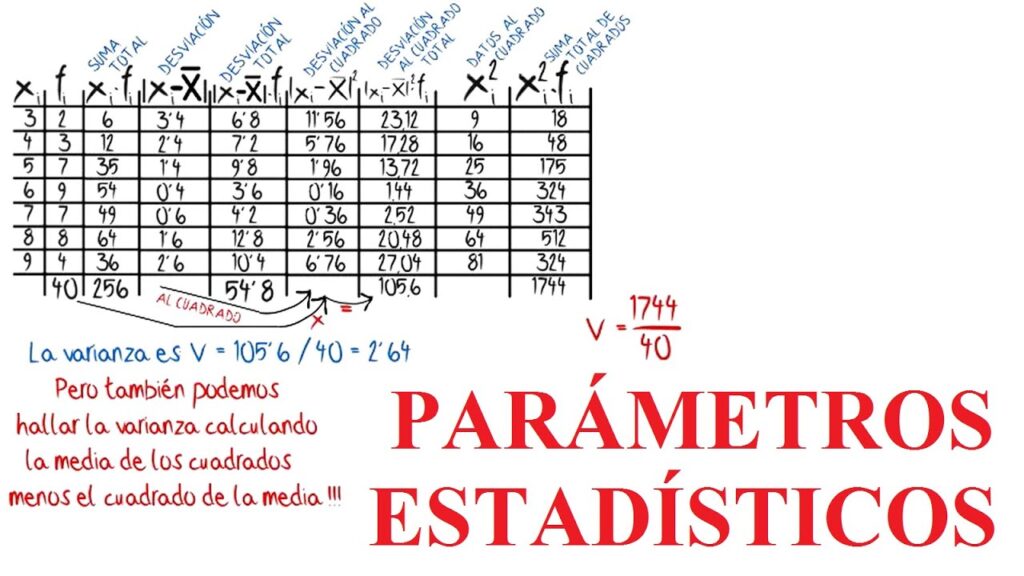
Varianza y Desviación Estándar: Medidas de Dispersión
Varianza
La varianza mide la dispersión de los datos alrededor de la media. Se calcula como el promedio de las diferencias al cuadrado entre cada valor y la media. La fórmula es:
Varianza (σ²) = Σ(X – μ)² / N
donde X es cada valor del conjunto de datos, μ es la media y N es el número de valores.
Desviación Estándar
La desviación estándar es la raíz cuadrada de la varianza. Es una medida más intuitiva de la dispersión porque está en las mismas unidades que los datos originales. La fórmula es:
Desviación Estándar (σ) = √σ²
Ambas medidas son útiles para entender la variabilidad de nuestros datos. Una alta desviación estándar indica que los datos están más dispersos, mientras que una baja desviación estándar indica que están más concentrados alrededor de la media.
Aplicaciones Prácticas de los Parámetros Estadísticos
Los parámetros estadísticos son herramientas poderosas y versátiles que se utilizan en una amplia variedad de campos, desde la investigación científica hasta el análisis de negocios. Veamos algunos ejemplos de cómo se pueden aplicar en la práctica.
Investigación Científica
En la investigación científica, los parámetros estadísticos son esenciales para analizar los resultados de los experimentos. Por ejemplo, en un estudio clínico, la media y la desviación estándar pueden ayudar a los investigadores a entender cómo responde un grupo de pacientes a un nuevo tratamiento.
Marketing y Negocios
En el mundo de los negocios, los parámetros estadísticos se utilizan para analizar el comportamiento del mercado y tomar decisiones informadas. Por ejemplo, la media puede ayudar a una empresa a entender el ingreso promedio de sus clientes, mientras que la desviación estándar puede proporcionar información sobre la variabilidad en los ingresos.
Educación
En el ámbito educativo, los parámetros estadísticos pueden ayudar a evaluar el rendimiento de los estudiantes. La media de las calificaciones puede proporcionar una visión general del rendimiento de una clase, mientras que la varianza puede indicar la diversidad de habilidades entre los estudiantes.
Comparación de Parámetros Estadísticos
Es importante entender cuándo utilizar cada parámetro estadístico, ya que cada uno tiene sus propias ventajas y limitaciones. Aquí hay una comparación rápida para ayudarte a decidir cuál es el más adecuado para tu análisis de datos:
- Media: Útil para conjuntos de datos simétricos sin valores atípicos. Puede ser influenciada por outliers.
- Mediana: Mejor para conjuntos de datos sesgados o con valores atípicos. No se ve afectada por outliers.
- Moda: Útil para entender la frecuencia de ocurrencia de un valor específico. No siempre es representativa del conjunto de datos.
- Varianza y Desviación Estándar: Importantes para entender la dispersión de los datos. Útiles en combinación con la media para una visión completa de los datos.
Recursos Adicionales
Si deseas profundizar en el tema de los parámetros estadísticos, te recomiendo consultar los siguientes recursos:
- Wikipedia – Estadística descriptiva
- Khan Academy – Statistics and Probability
- Coursera – Introduction to Statistics
Conclusión
Los parámetros estadísticos son herramientas esenciales para cualquier persona que trabaje con datos. Conocer y entender la media, la mediana, la moda, la varianza y la desviación estándar te permitirá analizar tus datos de manera más efectiva y tomar decisiones informadas. Espero que este artículo te haya proporcionado una visión clara y útil de estos conceptos. ¡No dudes en seguir explorando y practicando!
