Todo lo que necesitas saber
¿Qué son las ecuaciones cuadráticas y cúbicas?
Hola, soy Leandro, y hoy quiero hablarte sobre un tema que, aunque parezca complicado, es fundamental en el mundo de las matemáticas: las ecuaciones cuadráticas y cúbicas. A lo largo de mi carrera, he tenido la oportunidad de trabajar con estos tipos de ecuaciones y te aseguro que entenderlas puede marcar una gran diferencia en tu comprensión matemática.
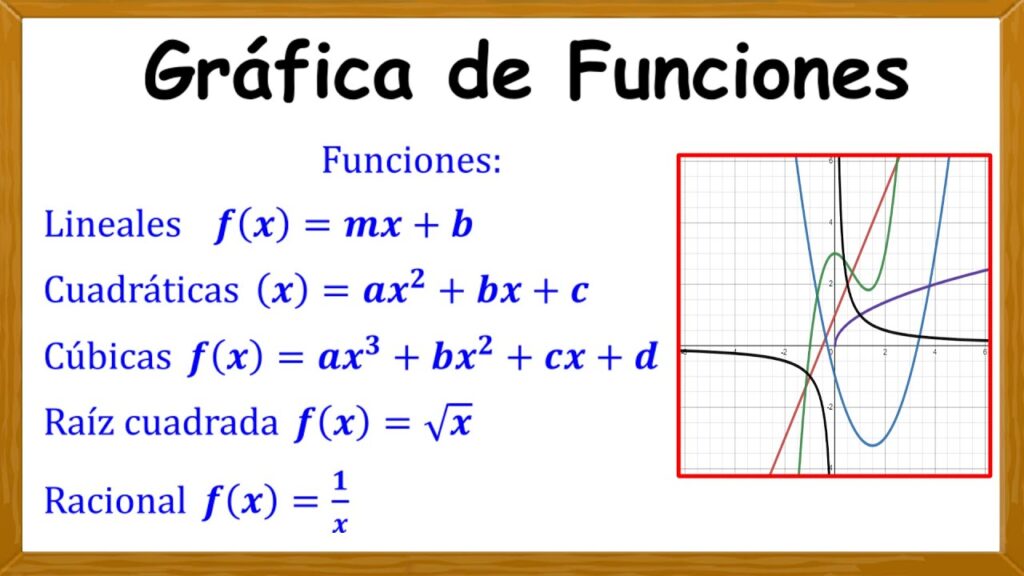
Las ecuaciones cuadráticas y cúbicas son polinomios de segundo y tercer grado respectivamente. En términos más simples, una ecuación cuadrática tiene la forma ax² + bx + c = 0, mientras que una ecuación cúbica tiene la forma ax³ + bx² + cx + d = 0. Aunque pueden parecer similares, su comportamiento y las técnicas para resolverlas son bastante diferentes.
Historia y aplicaciones de las ecuaciones cuadráticas
Un poco de historia
Las ecuaciones cuadráticas han sido estudiadas desde hace miles de años. Los antiguos babilonios ya conocían las soluciones a estas ecuaciones, y los matemáticos griegos como Euclides y Diofanto también hicieron importantes contribuciones. Sin embargo, fue en el siglo IX cuando el matemático persa Al-Khwarizmi escribió un tratado que sistematizó la solución de las ecuaciones cuadráticas, sentando las bases del álgebra moderna.
Aplicaciones en la vida cotidiana
Las ecuaciones cuadráticas tienen innumerables aplicaciones en la vida diaria. Desde la física hasta la economía, pasando por la ingeniería y la informática, estas ecuaciones son esenciales para modelar fenómenos que tienen una relación cuadrática entre las variables. Por ejemplo, en física, la ecuación de movimiento de un objeto en caída libre es una ecuación cuadrática.
Historia y aplicaciones de las ecuaciones cúbicas
Un poco de historia
Las ecuaciones cúbicas tienen una historia igualmente fascinante. Durante mucho tiempo, resolver ecuaciones cúbicas fue un problema que desconcertó a los matemáticos. Fue en el Renacimiento cuando los matemáticos italianos Scipione del Ferro, Tartaglia y Cardano lograron encontrar soluciones generales para estas ecuaciones.
Aplicaciones en la vida cotidiana
Las ecuaciones cúbicas también tienen muchas aplicaciones prácticas. Se utilizan en campos como la ingeniería, la economía y la física. Por ejemplo, en la ingeniería, se utilizan para diseñar curvas y superficies en tres dimensiones. En economía, las ecuaciones cúbicas pueden modelar la oferta y la demanda de productos.
Diferencias clave entre ecuaciones cuadráticas y cúbicas
Grado del polinomio
La diferencia más obvia entre las ecuaciones cuadráticas y cúbicas es el grado del polinomio. Las ecuaciones cuadráticas son de segundo grado, mientras que las cúbicas son de tercer grado. Esta diferencia en el grado afecta la forma de las gráficas y el número de soluciones posibles.
Soluciones posibles
Una ecuación cuadrática puede tener hasta dos soluciones reales, mientras que una ecuación cúbica puede tener hasta tres soluciones reales. Esto se debe a la forma en que los polinomios se cruzan con el eje x.
Complejidad de la resolución
Resolver ecuaciones cuadráticas es relativamente sencillo gracias a la fórmula cuadrática, que proporciona una solución directa. Sin embargo, las ecuaciones cúbicas son más complicadas y requieren técnicas más avanzadas, como el método de Cardano o la factorización.
¿Cuál es mejor: ecuaciones cuadráticas o cúbicas?
Depende del contexto
La pregunta de cuál es mejor, si las ecuaciones cuadráticas o las cúbicas, no tiene una respuesta sencilla. Todo depende del contexto y de lo que estés tratando de modelar o resolver. En general, las ecuaciones cuadráticas son más fáciles de manejar y solucionar, pero las ecuaciones cúbicas ofrecen una mayor flexibilidad y pueden modelar fenómenos más complejos.
Facilidad de uso
Si buscas facilidad de uso y rapidez en la resolución, las ecuaciones cuadráticas son la mejor opción. La fórmula cuadrática te permite encontrar las soluciones de manera directa y rápida.
Modelado de fenómenos complejos
Si necesitas modelar fenómenos más complejos, las ecuaciones cúbicas son más adecuadas. Aunque son más difíciles de resolver, ofrecen una mayor flexibilidad y pueden capturar más detalles en el comportamiento de las variables.
Recursos adicionales para aprender más sobre ecuaciones cuadráticas y cúbicas
Para aquellos que deseen profundizar más en el tema de las ecuaciones cuadráticas y cúbicas, aquí hay algunos recursos adicionales que podrían ser de gran ayuda:
