Divisibilidad: Una Guía Completa por Leandro
Introducción a la Divisibilidad
Hola, soy Leandro, y hoy vamos a sumergirnos en el fascinante mundo de la divisibilidad. Quizás te preguntes, ¿qué tiene de fascinante? Pues, déjame decirte que es uno de los pilares fundamentales de las matemáticas, y entenderlo puede cambiar tu forma de ver los números.
¿Qué es la Divisibilidad?
La divisibilidad es una propiedad de los números que indica si un número entero puede ser dividido por otro sin dejar residuo. Por ejemplo, el número 10 es divisible por 2 y 5, ya que 10 dividido por 2 da 5, y 10 dividido por 5 da 2, ambos sin dejar residuo.
En términos más técnicos, decimos que un número a es divisible por un número b si existe un número entero c tal que a = b * c. Si esto se cumple, entonces b es un divisor de a, y a es un múltiplo de b.
Conceptos Clave en Divisibilidad
Divisores y Múltiplos
Los divisores de un número son aquellos números que lo pueden dividir exactamente. Por ejemplo, los divisores de 12 son 1, 2, 3, 4, 6 y 12.
Los múltiplos de un número son los resultados de multiplicar ese número por otros números enteros. Por ejemplo, los primeros múltiplos de 5 son 5, 10, 15, 20, y así sucesivamente.
Números Primos
Un número primo es aquel que solo tiene dos divisores: 1 y él mismo. Algunos ejemplos son 2, 3, 5, 7, 11, entre otros. Los números primos juegan un papel crucial en la teoría de números y la divisibilidad.
Reglas de Divisibilidad
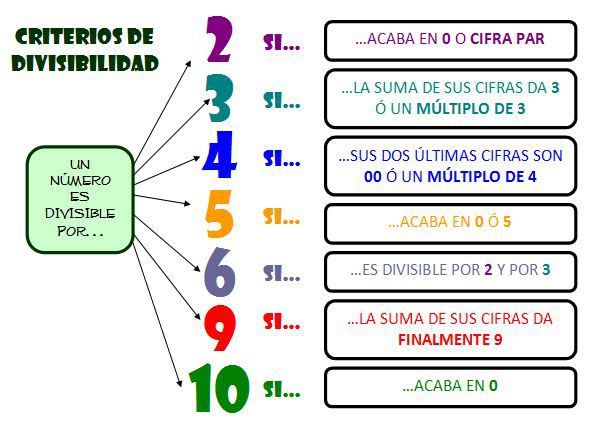
Existen reglas simples que nos permiten determinar rápidamente si un número es divisible por otro sin necesidad de realizar la división completa. A continuación, exploraremos algunas de las más comunes:
Divisibilidad por 2
Un número es divisible por 2 si su último dígito es 0, 2, 4, 6 u 8. Ejemplo: 18 es divisible por 2.
Divisibilidad por 3
Un número es divisible por 3 si la suma de sus dígitos es divisible por 3. Ejemplo: 123 es divisible por 3 (1 + 2 + 3 = 6, y 6 es divisible por 3).
Divisibilidad por 5
Un número es divisible por 5 si termina en 0 o 5. Ejemplo: 25 es divisible por 5.
Divisibilidad por 7
Para verificar la divisibilidad por 7, se recomienda un método más complejo: se duplica el último dígito y se resta del número formado por los dígitos restantes. Si el resultado es divisible por 7, entonces el número original también lo es. Ejemplo: 133 (3 * 2 = 6; 13 – 6 = 7, y 7 es divisible por 7).
Divisibilidad por 11
Un número es divisible por 11 si la diferencia entre la suma de sus dígitos en posiciones impares y la suma de sus dígitos en posiciones pares es múltiplo de 11. Ejemplo: 121 (1 – 2 + 1 = 0, y 0 es múltiplo de 11).
Aplicaciones Prácticas de la Divisibilidad
La divisibilidad tiene numerosas aplicaciones prácticas en distintas áreas de las matemáticas y la vida diaria. Algunos ejemplos incluyen:
Fracciones y Simplificación
La divisibilidad es esencial para simplificar fracciones. Al conocer los divisores de los numeradores y denominadores, podemos reducir las fracciones a su forma más simple. Ejemplo: 16/24 se simplifica a 2/3 al dividir ambos por 8.
Criptografía
En criptografía, los números primos y la divisibilidad juegan un papel crucial en la creación de claves seguras. Los algoritmos de encriptación, como RSA, se basan en la dificultad de factorizar grandes números primos.
Teoría de Números
La teoría de números, una rama de las matemáticas puras, estudia las propiedades de los números enteros y su divisibilidad. Esta área tiene aplicaciones en la informática, la física y otras ciencias.
Comparación con Otros Conceptos Relacionados
Es común confundir la divisibilidad con otros conceptos matemáticos relacionados. A continuación, aclararemos algunas diferencias clave:
Divisibilidad vs. Divisores Comunes
Mientras que la divisibilidad se refiere a si un número puede dividir a otro sin dejar residuo, los divisores comunes son aquellos números que pueden dividir a dos o más números. Por ejemplo, los divisores comunes de 12 y 18 son 1, 2, 3 y 6.
Divisibilidad vs. Múltiplos Comunes
Los múltiplos comunes son aquellos números que son múltiplos de dos o más números. Por ejemplo, los múltiplos comunes de 3 y 4 son 12, 24, 36, etc. La divisibilidad y los múltiplos comunes están estrechamente relacionados, pero no son lo mismo.
Divisibilidad vs. Factorización
La factorización consiste en descomponer un número en sus factores primos. Aunque la divisibilidad es una parte esencial de este proceso, la factorización es un concepto más amplio que incluye la identificación de todos los divisores de un número.
Recursos Adicionales y Enlaces Relacionados
Para aquellos que deseen profundizar en el tema de la divisibilidad, aquí hay algunos recursos adicionales que pueden resultar útiles:
Conclusión
La divisibilidad es un concepto fundamental en matemáticas que nos permite entender mejor la estructura y propiedades de los números. Desde simplificar fracciones hasta aplicaciones en criptografía, la divisibilidad es una herramienta poderosa y versátil.
Espero que este artículo haya sido útil para aclarar tus dudas y ampliar tu conocimiento sobre la divisibilidad. Si tienes alguna pregunta o comentario, no dudes en dejarlo abajo. ¡Hasta la próxima!
