Distribuciones de Frecuencia y Medidas de Tendencia Central
Introducción a las Distribuciones de Frecuencia y Medidas de Tendencia Central
¡Hola! Soy Leandro y hoy vamos a sumergirnos en el fascinante mundo de las distribuciones de frecuencia y las medidas de tendencia central. Si alguna vez te has preguntado cómo analizar datos de manera eficiente, estás en el lugar correcto. Como alguien que ha pasado años trabajando con estadísticas, estoy aquí para desmitificar estos conceptos y mostrarte cómo pueden ser tus mejores amigos en el análisis de datos.
¿Qué son las Distribuciones de Frecuencia?
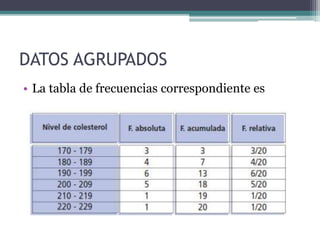
Empecemos por las distribuciones de frecuencia. En términos simples, una distribución de frecuencia es una tabla que muestra el número de ocurrencias de diferentes valores en un conjunto de datos. Es una herramienta fundamental para entender cómo se distribuyen los datos en un estudio.
Para crear una distribución de frecuencia, primero necesitas un conjunto de datos. Luego, divides estos datos en clases o intervalos y cuentas cuántos datos caen en cada intervalo. Esto te dará una idea clara de la distribución de tus datos.
Importancia de las Distribuciones de Frecuencia
Las distribuciones de frecuencia son cruciales porque nos ayudan a visualizar la distribución de los datos de una manera comprensible. Permiten identificar patrones, tendencias y anomalías dentro del conjunto de datos. Además, son el primer paso para aplicar otras técnicas estadísticas, como el cálculo de medidas de tendencia central.
Medidas de Tendencia Central: Una Visión General
Ahora que entendemos las distribuciones de frecuencia, pasemos a las medidas de tendencia central. Estas son valores que intentan describir un conjunto de datos identificando el valor central dentro de esa distribución. Las tres medidas de tendencia central más comunes son la media, la mediana y la moda.
La Media: El Valor Promedio
La media, también conocida como promedio, es quizás la medida de tendencia central más conocida. Se calcula sumando todos los valores del conjunto de datos y dividiendo el resultado entre el número total de valores. La fórmula es simple:
Media = (Σx) / N
donde Σx es la suma de todos los valores y N es el número total de valores.
La media es muy útil, pero puede ser engañosa si hay valores extremadamente altos o bajos en el conjunto de datos, ya que estos pueden sesgar el promedio.
La Mediana: El Valor del Medio
La mediana es el valor que se encuentra en el medio de un conjunto de datos ordenados. Si el número de datos es impar, la mediana es el valor central. Si el número de datos es par, la mediana es el promedio de los dos valores centrales.
Una de las principales ventajas de la mediana es que no se ve afectada por valores extremadamente altos o bajos, lo que la hace una medida robusta de tendencia central.
La Moda: El Valor Más Frecuente
La moda es el valor que ocurre con mayor frecuencia en un conjunto de datos. A diferencia de la media y la mediana, un conjunto de datos puede tener más de una moda (bimodal, trimodal, etc.) o no tener ninguna moda.
La moda es especialmente útil en conjuntos de datos categóricos donde queremos identificar la categoría más común.
Comparación entre Media, Mediana y Moda
Cada una de estas medidas de tendencia central tiene sus propias ventajas y desventajas. La media es útil para conjuntos de datos simétricos sin valores extremos. La mediana es más adecuada para conjuntos de datos sesgados o con valores extremos. La moda es ideal para datos categóricos.
Elegir la medida adecuada depende del tipo de datos que tienes y de lo que quieres lograr con tu análisis.
Cómo Interpretar las Distribuciones de Frecuencia y Medidas de Tendencia Central
Una vez que tienes tus distribuciones de frecuencia y medidas de tendencia central, ¿Cómo las interpretas? Aquí es donde entra en juego la experiencia y el contexto. Es crucial entender el contexto de tus datos para hacer interpretaciones significativas.
Por ejemplo, si estás analizando las calificaciones de estudiantes en un examen, una media alta podría indicar un buen desempeño general, pero una mediana baja podría revelar que la mayoría de los estudiantes no está rindiendo bien.
Aplicaciones Prácticas de Distribuciones de Frecuencia y Medidas de Tendencia Central
Las distribuciones de frecuencia y las medidas de tendencia central son herramientas increíblemente versátiles. Se utilizan en una variedad de campos, desde la investigación académica hasta los negocios y el análisis de mercado.
En el mundo empresarial, estas herramientas pueden ayudar a identificar tendencias de consumo, evaluar el desempeño de productos y tomar decisiones informadas basadas en datos. En la investigación académica, son esenciales para analizar resultados experimentales y validar hipótesis.
Recursos Adicionales y Lecturas Recomendadas
Si te interesa profundizar en este tema, te recomiendo algunos recursos adicionales:
Conclusión: El Poder de las Distribuciones de Frecuencia y Medidas de Tendencia Central
En resumen, las distribuciones de frecuencia y las medidas de tendencia central son fundamentales para cualquier análisis de datos. Nos permiten comprender y visualizar nuestros datos de una manera que facilita la toma de decisiones informadas.
Espero que este artículo te haya proporcionado una comprensión clara y práctica de estos conceptos. Recuerda, la clave está en elegir la herramienta adecuada para tu conjunto de datos específico. ¡Feliz análisis!
