Introducción al Principio de Inclusión y Exclusión
¡Hola a todos! Soy Leandro, y hoy quiero hablarles sobre un tema que puede sonar un poco complicado al principio, pero que es increíblemente útil una vez que lo entiendes: el Principio de Inclusión y Exclusión. Este principio es una herramienta fundamental en la teoría de conjuntos y la combinatoria, y tiene aplicaciones prácticas que van desde el cálculo de probabilidades hasta la optimización de algoritmos.
¿Qué es el Principio de Inclusión y Exclusión?
El Principio de Inclusión y Exclusión es una técnica matemática utilizada para contar el número de elementos en la unión de varios conjuntos. Suena complicado, ¿verdad? Vamos a desglosarlo un poco.
Imagina que tienes dos conjuntos, A y B. Si quieres saber cuántos elementos hay en la unión de A y B (es decir, en A ∪ B), no puedes simplemente sumar el número de elementos en A y el número de elementos en B. ¿Por qué? Porque los elementos que están en ambos conjuntos se contarían dos veces.
El Principio de Inclusión y Exclusión nos dice que para encontrar el número de elementos en A ∪ B, debemos sumar los elementos de A y B, pero luego restar los elementos que están en ambos conjuntos. Matemáticamente, esto se expresa como:
|A ∪ B| = |A| + |B| – |A ∩ B|
Aplicaciones del Principio de Inclusión y Exclusión
Este principio no solo es útil en teoría, sino que tiene varias aplicaciones prácticas. Aquí hay algunas de las más comunes:
1. Cálculo de Probabilidades
En el campo de las probabilidades, este principio ayuda a calcular la probabilidad de la unión de eventos. Por ejemplo, si quieres saber la probabilidad de que ocurra al menos uno de dos eventos, puedes usar este principio para evitar el doble conteo de la intersección de esos eventos.
2. Optimización de Algoritmos
En informática, el Principio de Inclusión y Exclusión se utiliza para optimizar algoritmos que cuentan elementos en grandes conjuntos. Por ejemplo, se puede aplicar en problemas de bases de datos y en la búsqueda de patrones en grandes volúmenes de datos.
Ejemplos Prácticos del Principio de Inclusión y Exclusión
Para entender mejor cómo funciona este principio, vamos a ver algunos ejemplos prácticos.
Ejemplo 1: Calculando la Unión de Tres Conjuntos
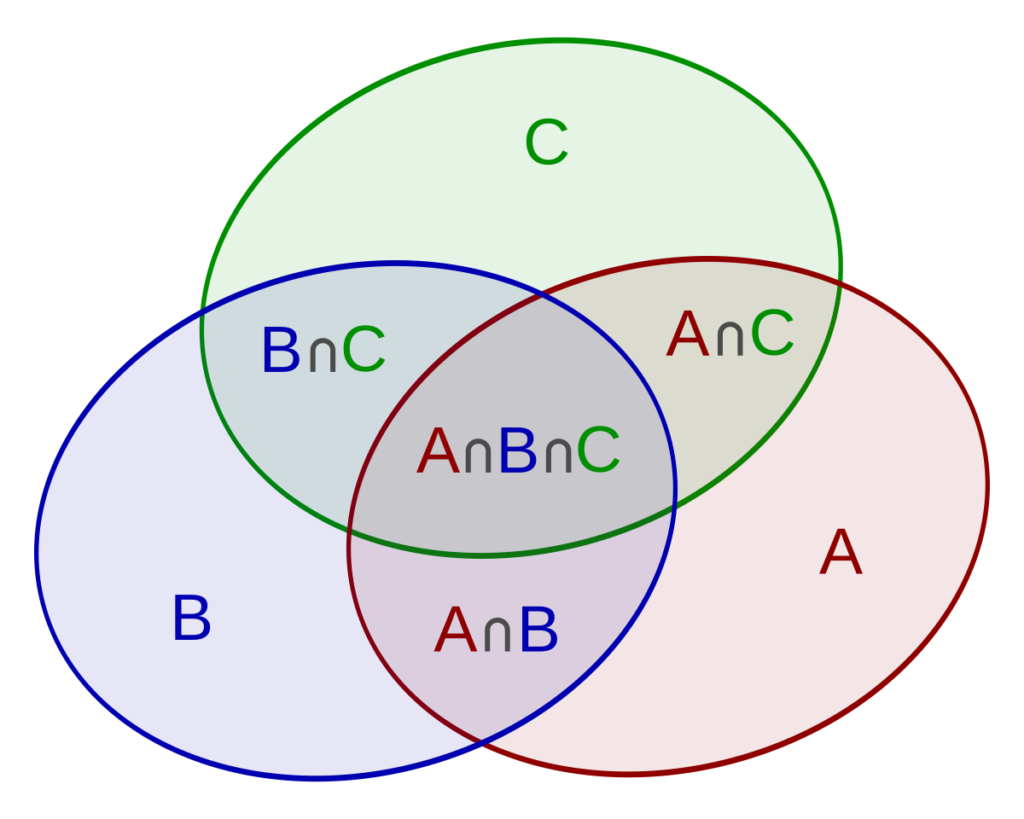
Supongamos que tienes tres conjuntos A, B y C. El Principio de Inclusión y Exclusión se puede extender para tres conjuntos de la siguiente manera:
|A ∪ B ∪ C| = |A| + |B| + |C| – |A ∩ B| – |A ∩ C| – |B ∩ C| + |A ∩ B ∩ C|
Este cálculo asegura que los elementos que están en la intersección de dos conjuntos no se cuenten dos veces, y que los elementos en la intersección de los tres conjuntos se cuenten nuevamente.
Comparación con Otros Métodos y Herramientas
Es natural preguntarse si hay otros métodos que puedan hacer lo mismo que el Principio de Inclusión y Exclusión, y cuál de ellos es mejor. Vamos a explorar algunas alternativas.
Métodos Alternativos
Uno de los métodos más comunes para contar elementos en conjuntos es el uso de diagramas de Venn. Los diagramas de Venn son visualmente intuitivos y pueden ser útiles para problemas simples. Sin embargo, se vuelven menos prácticos a medida que aumenta el número de conjuntos.
Recursos Adicionales y Enlaces Relacionados
Si este artículo te ha despertado la curiosidad y quieres aprender más sobre el Principio de Inclusión y Exclusión, aquí tienes algunos recursos adicionales:
