Permutaciones – Explicado a profundidad
Introducción a las Permutación
Hola, soy Leandro y hoy quiero hablarles sobre un tema fascinante en el mundo de las matemáticas: las permutaciones. Este concepto puede sonar complicado al principio, pero les aseguro que con un poco de explicación y ejemplos claros, será mucho más fácil de entender.
Las permutaciones son una forma específica de ordenar un conjunto de elementos. A diferencia de las combinaciones, donde el orden no importa, en las permutaciones el orden es crucial. Por ejemplo, si tenemos los elementos A, B y C, las permutaciones serían ABC, ACB, BAC, BCA, CAB y CBA.
¿Qué son las Permutaciones?
En términos matemáticos, una permutación es una disposición de todos los elementos de un conjunto en un orden específico. Se puede pensar en esto como la reordenación de las letras en una palabra. Por ejemplo, las permutaciones de las letras en la palabra «GATO» incluirían «GATO», «GOTA», «AGOT», «ATOG», etc.
El número total de permutaciones de un conjunto de n elementos se denota por n! (factorial de n) y se calcula multiplicando todos los números enteros positivos hasta n. Por ejemplo, para un conjunto de 3 elementos, el número de permutaciones sería 3! = 3 × 2 × 1 = 6.
Tipos de Permutaciones
Permutaciones sin Repetición
Las permutaciones sin repetición son aquellas en las que cada elemento aparece una sola vez. Por ejemplo, para los elementos A, B y C, las permutaciones sin repetición serían ABC, ACB, BAC, BCA, CAB y CBA.
Permutaciones con Repetición
En las permutaciones con repetición, algunos elementos pueden repetirse. Por ejemplo, si tenemos los elementos A, A y B, las permutaciones con repetición serían AAB, ABA y BAA. El número de permutaciones con repetición se calcula de manera diferente y depende de la cantidad de repeticiones de cada elemento.
Aplicaciones de las Permutaciones
Las permutaciones tienen una amplia gama de aplicaciones en diversas áreas, desde la biología hasta la informática. A continuación, mencionaré algunas de las aplicaciones más comunes:
Permutaciones en la Biología
En biología, las permutaciones se utilizan para estudiar las posibles combinaciones de genes y la variabilidad genética. Por ejemplo, al analizar la secuencia de ADN, los científicos pueden utilizar permutaciones para determinar todas las posibles combinaciones de bases nitrogenadas.
Permutaciones en la Informática
En informática, las permutaciones son fundamentales en algoritmos de búsqueda y ordenación. Por ejemplo, en el algoritmo de ordenación por permutación, se generan todas las posibles permutaciones de un conjunto de datos y se ordenan para encontrar la solución óptima.
Permutaciones en la Estadística
En estadística, las permutaciones se utilizan para calcular probabilidades y analizar datos. Por ejemplo, en el análisis de datos de encuestas, las permutaciones pueden ayudar a determinar todas las posibles combinaciones de respuestas y calcular la probabilidad de ciertos resultados.
Cómo Calcular Permutaciones
Fórmula de Permutaciones
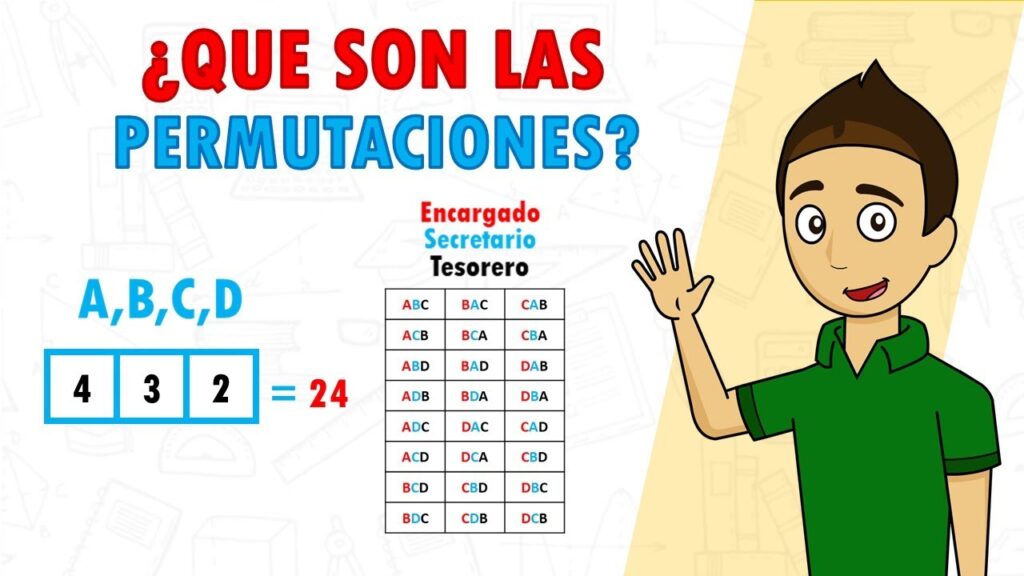
La fórmula general para calcular el número de permutaciones de un conjunto de n elementos es n!. Por ejemplo, para un conjunto de 4 elementos, el número de permutaciones sería 4! = 4 × 3 × 2 × 1 = 24.
Permutaciones con Repetición
Para calcular el número de permutaciones con repetición, se utiliza la fórmula n! / (p1! × p2! × … × pk!), donde n es el número total de elementos y p1, p2, …, pk son las cantidades de cada elemento repetido. Por ejemplo, para los elementos A, A y B, el número de permutaciones con repetición sería 3! / (2! × 1!) = 3.
Desafíos y Problemas Comunes al Trabajar con Permutaciones
Trabajar con permutaciones puede presentar algunos desafíos y problemas comunes. A continuación, mencionaré algunos de ellos y cómo pueden abordarse:
Problemas de Escalabilidad
A medida que el número de elementos en un conjunto aumenta, el número de permutaciones crece exponencialmente. Esto puede hacer que el cálculo de permutaciones sea computacionalmente costoso y difícil de manejar para conjuntos grandes. Para abordar este problema, se pueden utilizar algoritmos de optimización y técnicas de reducción de complejidad.
Errores de Cálculo
Es fácil cometer errores al calcular permutaciones, especialmente cuando se trabaja con fórmulas complejas y grandes cantidades de datos. Para evitar errores de cálculo, es importante verificar y validar los resultados utilizando métodos alternativos y herramientas de software.
Interpretación de Resultados
Interpretar los resultados de las permutaciones puede ser complicado, especialmente en contextos donde las permutaciones tienen significados específicos. Para interpretar los resultados correctamente, es importante tener un buen conocimiento del contexto y de las implicaciones de las permutaciones en ese contexto.
Recursos y Herramientas Útiles
Hay muchos recursos y herramientas disponibles para ayudar a comprender y trabajar con permutaciones. A continuación, mencionaré algunos de los más útiles:
Libros y Artículos
Existen muchos libros y artículos que abordan el tema de las permutaciones en profundidad. Algunos de los más recomendados incluyen «Permutations and Combinations» de L. Comtet y «An Introduction to Combinatorial Analysis» de J. Riordan.
Software y Herramientas en Línea
Hay varias herramientas de software y recursos en línea que pueden ayudar a calcular y visualizar permutaciones. Algunas de las más populares incluyen:
- Wolfram Alpha: Una herramienta computacional que puede calcular permutaciones y combinaciones.
- Symbolab: Una calculadora matemática en línea que ofrece funciones para calcular permutaciones.
- GeoGebra: Un software de matemáticas dinámicas que incluye herramientas para trabajar con permutaciones.
Conclusión
Las permutaciones son un concepto fundamental en matemáticas con aplicaciones en diversas áreas, desde la biología hasta la informática. Aunque pueden parecer complicadas al principio, con una comprensión clara de los conceptos y las fórmulas, es posible trabajar con permutaciones de manera efectiva. Espero que este artículo les haya proporcionado una buena introducción a las permutaciones y les haya ayudado a comprender mejor este fascinante tema.
