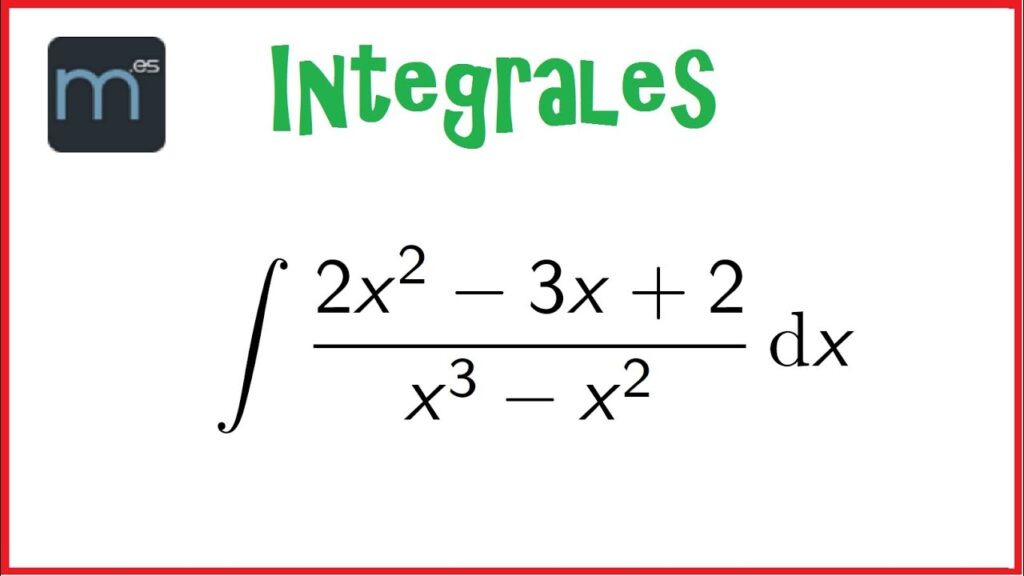
Integrales Racionales: Domina el Arte de la Integración con Estilo

¡Saludos, apasionados de las matemáticas y buscadores del saber integrador! Soy Leandro, y hoy nos sumergiremos en el fascinante mundo de las integrales racionales. ¿Qué son, te preguntas? Bueno, no te preocupes, porque voy a guiarte a través de este océano de fracciones y potencias para que salgas navegando con conocimiento y estilo.

Introducción a las Integrales Racionales

Las integrales racionales son un tipo especial de integral en la que la función integrando es una fracción polinómica. Es decir, tenemos un polinomio en el numerador y otro en el denominador. ¿Por qué son tan interesantes? Porque nos permiten resolver una amplia gama de problemas matemáticos y aplicaciones prácticas, desde la física hasta la economía.

Componentes de una Integral Racional

Para entender mejor cómo funciona una integral racional, es esencial conocer sus componentes básicos:

1. Numerador y Denominador Polinómicos: La función a integrar tiene la forma P(x)Q(x)\frac{P(x)}{Q(x)}Q(x)P(x)​, donde $P(x)$ y $Q(x)$ son polinomios.

2. Raíces del Denominador: Las raíces del polinomio $Q(x)$ determinan los puntos donde la función tiene singularidades o puntos donde la integral puede presentar discontinuidades.

Técnicas de Integración

Ahora, ¿cómo abordamos la integración de estas expresiones tan particulares? Aquí van algunas técnicas clave:

Descomposición en Fracciones Parciales

La técnica más común y poderosa para integrar integrales racionales es la descomposición en fracciones parciales. Esto implica expresar P(x)Q(x)\frac{P(x)}{Q(x)}Q(x)P(x)​ como una suma de fracciones simples cuyos denominadores son potencias de factores lineales e irreducibles de $Q(x)$.

Cambio de Variable y Simplificación

En algunos casos, realizar un cambio de variable puede simplificar la integral racional, convirtiéndola en una forma más manejable. Esto es especialmente útil cuando el grado de $P(x)$ es menor que el grado de $Q(x)$.

Aplicaciones en la Vida Real

Las integrales racionales no solo son un ejercicio teórico, sino que tienen aplicaciones directas en diversas áreas:

• Economía y Finanzas: Modelado de tasas de interés, devaluaciones monetarias, entre otros.

• Física: Cálculo de trabajo realizado, centro de masa, momento de inercia, entre otros.

• Ingeniería: Análisis de circuitos eléctricos, control de procesos industriales, entre otros.

Conclusión

En resumen, las integrales racionales son una herramienta poderosa en el arsenal de cualquier matemático o científico. Dominar su técnica no solo amplía nuestras habilidades analíticas, sino que también abre puertas a nuevas aplicaciones y descubrimientos en el mundo de las ciencias exactas. Así que, ¡anímate a explorar este fascinante campo y a conquistar las integrales racionales con determinación y gracia!

Espero que este recorrido te haya sido útil y entretenido. Hasta la próxima aventura matemática, ¡Leandro se despide!