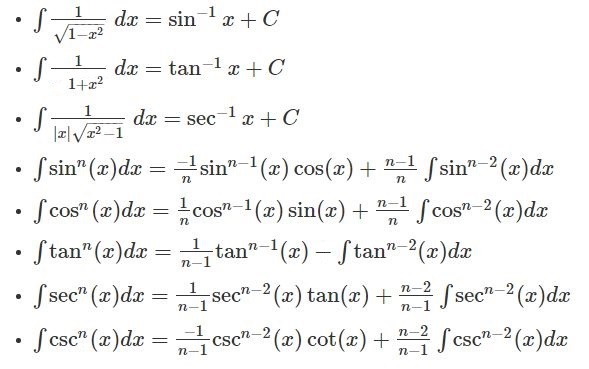
Integrales Fórmulas – Una Guía Completa
Introducción a las Integrales y sus Fórmulas
¡Hola! Soy Leandro, un apasionado del cálculo y las matemáticas. Hoy quiero compartir contigo todo lo que sé sobre las integrales y sus fórmulas. Este tema puede parecer un poco intimidante al principio, pero te aseguro que con un poco de paciencia y dedicación, podrás dominarlo.
Las integrales son una parte fundamental del cálculo y tienen aplicaciones en diversas áreas como la física, la ingeniería e incluso la economía. En este artículo, exploraremos las fórmulas de integrales más comunes, sus usos y cómo puedes aplicarlas en diferentes contextos.
¿Qué son las Integrales?
Antes de profundizar en las fórmulas de integrales, es importante entender qué son las integrales. En términos sencillos, una integral es una operación matemática que nos permite calcular el área bajo una curva. En otras palabras, es una forma de sumar infinitas cantidades infinitesimales.
Existen dos tipos principales de integrales: las integrales definidas y las integrales indefinidas. Las integrales definidas tienen límites específicos y nos permiten calcular un valor numérico exacto. Por otro lado, las integrales indefinidas no tienen límites y nos proporcionan una función general.
Fórmulas Básicas de Integrales
Integral de una Constante
Una de las fórmulas de integrales más básicas es la integral de una constante. Si tienes una constante c, su integral es simplemente c multiplicada por la variable de integración, más una constante de integración (C).
Fórmula: ∫c dx = cx + C
Integral de una Función Potencia
Otra fórmula fundamental es la integral de una función potencia. Si tienes una función de la forma xn, su integral es (xn+1)/(n+1), más la constante de integración (C).
Fórmula: ∫xn dx = (xn+1)/(n+1) + C (con n ≠ -1)
Fórmulas Avanzadas de Integrales
Integral de Funciones Trigonométricas
Las funciones trigonométricas también tienen sus propias fórmulas de integrales. Aquí te dejo algunas de las más comunes:
∫sin(x) dx = -cos(x) + C∫cos(x) dx = sin(x) + C∫tan(x) dx = -ln|cos(x)| + C
Integral de la Función Exponencial
La función exponencial es otra función importante en el cálculo. La integral de la función exponencial ex es simplemente ex, más la constante de integración (C).
Fórmula: ∫ex dx = ex + C
Aplicaciones de las Integrales
Las fórmulas de integrales no son solo un concepto abstracto; tienen muchas aplicaciones prácticas. Aquí te dejo algunas de las áreas donde las integrales son extremadamente útiles:
Física
En física, las integrales se utilizan para calcular cosas como el trabajo realizado por una fuerza, el área bajo una curva de velocidad-tiempo para hallar la distancia recorrida, y mucho más.
Ingeniería
En ingeniería, las integrales son esenciales para el diseño y análisis de sistemas. Por ejemplo, se utilizan para calcular el centro de masa, el momento de inercia y en el análisis de circuitos eléctricos.
Economía
En economía, las integrales se usan para calcular el costo total y el ingreso total, entre otras cosas. Por ejemplo, si conoces la función de costo marginal, puedes integrar para encontrar el costo total.
Recursos Adicionales
Si quieres profundizar más en el tema de las integrales y sus fórmulas, te recomiendo visitar los siguientes enlaces:
Conclusión
Espero que este artículo te haya ayudado a entender mejor las fórmulas de integrales y su importancia. Recuerda que la práctica es clave, así que no dudes en resolver muchos problemas para familiarizarte con estos conceptos.
Si tienes alguna pregunta o comentario, no dudes en dejarlo abajo. Estoy aquí para ayudarte en tu viaje por el fascinante mundo del cálculo.
