Introducción a las Aplicaciones de la Integral Definida
Hola, soy Leandro y hoy voy a hablar sobre las aplicaciones de la integral definida. A lo largo de mi carrera, he tenido la oportunidad de ver cómo esta herramienta matemática puede ser increíblemente útil en diversas disciplinas. La integral definida no es solo un concepto abstracto que aprendemos en matemáticas; tiene aplicaciones prácticas que van desde la física y la ingeniería hasta la economía y las ciencias sociales.
¿Qué es la Integral Definida?
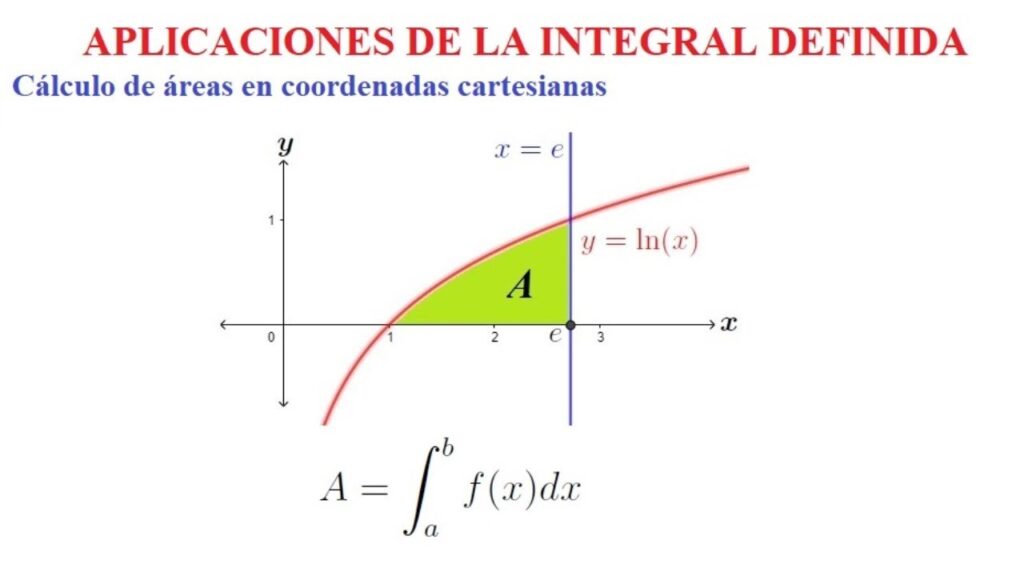
Para aquellos que no están familiarizados, la integral definida es una operación matemática que permite calcular el área bajo una curva en un intervalo específico. En términos más técnicos, es el límite de una suma de áreas de rectángulos bajo una curva, a medida que el tamaño de los rectángulos se aproxima a cero. Matematicamente, se representa como:
(int_{a}^{b} f(x) dx)
Aquí, (f(x)) es una función continua en el intervalo ([a, b]), y la integral definida de (f(x)) desde (a) hasta (b) se denota como (int_{a}^{b} f(x) dx).
Aplicaciones de la Integral Definida en Física
La física es uno de los campos donde más se utilizan las integrales definidas. Aquí te muestro algunas aplicaciones destacadas:
Cálculo del Trabajo
En física, el trabajo realizado por una fuerza constante se calcula como el producto de la fuerza y la distancia. Sin embargo, cuando la fuerza varía a lo largo del camino, utilizamos la integral definida para calcular el trabajo. La fórmula básica para el trabajo es:
( W = int_{a}^{b} F(x) dx )
Donde ( F(x) ) es la fuerza en función de la posición ( x ).
Centro de Masa
El centro de masa de un objeto se puede calcular utilizando integrales definidas. Para un objeto con densidad variable, la posición del centro de masa se da por:
( bar{x} = frac{int_{a}^{b} x cdot rho(x) dx}{int_{a}^{b} rho(x) dx} )
Aquí, ( rho(x) ) es la densidad del objeto en función de la posición ( x ).
Aplicaciones de la Integral Definida en Ingeniería
La ingeniería es otro campo que se beneficia enormemente de las integrales definidas. Vamos a ver algunas aplicaciones:
Análisis de Esfuerzos y Deformaciones
En ingeniería estructural, las integrales definidas se utilizan para calcular los esfuerzos y deformaciones en materiales. Por ejemplo, la deformación de una viga bajo una carga se puede determinar mediante la integral de la curva de momento flector.
Flujo de Fluidos
En ingeniería de fluidos, las integrales definidas se utilizan para calcular el flujo de un fluido a través de una sección transversal. La ecuación básica es:
( Q = int_{A} v cdot dA )
Dónde ( Q ) es el caudal, ( v ) es la velocidad del fluido y ( dA ) es un elemento diferencial de área.
Aplicaciones de la Integral Definida en Economía
La economía también se beneficia de las integrales definidas, especialmente en el análisis de costos y beneficios. Aquí algunos ejemplos:
Beneficio Total
Para calcular el beneficio total obtenido por una empresa, se puede utilizar la integral definida de la función de ingresos menos la función de costos:
( B = int_{a}^{b} (I(x) – C(x)) dx )
Aquí, ( I(x) ) es la función de ingresos y ( C(x) ) es la función de costos.
Costo Total
El costo total incurrido en la producción de una cantidad ( q ) de bienes se puede calcular utilizando la integral definida de la función de costo marginal:
( TC = int_{0}^{q} MC(x) dx )
Dónde ( MC(x) ) es el costo marginal.
Aplicaciones de la Integral Definida en Ciencias Sociales
En ciencias sociales, las integrales definidas se utilizan principalmente en el análisis de datos y la modelización de fenómenos sociales. Aquí algunos ejemplos:
Distribución de Población
Las integrales definidas se pueden utilizar para calcular la distribución de la población en un área específica. Si ( p(x) ) es la densidad de población en función de la posición ( x ), entonces la población total en un intervalo ([a, b]) es:
( P = int_{a}^{b} p(x) dx )
Modelos de Crecimiento
Los modelos de crecimiento poblacional o económico a menudo utilizan integrales definidas para predecir el crecimiento futuro. Por ejemplo, si ( r(t) ) es la tasa de crecimiento en función del tiempo, entonces la población en el tiempo ( T ) es:
( P(T) = P_0 + int_{0}^{T} r(t) dt )
Aquí, ( P_0 ) es la población inicial.
Aplicaciones de la Integral Definida en la Estadística
En estadística, las integrales definidas juegan un papel crucial en la teoría de probabilidades y en el análisis de datos. Veamos algunos ejemplos:
Función de Distribución Acumulativa
La función de distribución acumulativa (FDA) de una variable aleatoria continua se define mediante una integral definida. Si ( f(x) ) es la función de densidad de probabilidad, entonces la FDA ( F(x) ) es:
( F(x) = int_{-infty}^{x} f(t) dt )
Esperanza Matemática
La esperanza matemática o valor esperado de una variable aleatoria continua se calcula utilizando una integral definida. Si ( X ) es una variable aleatoria con función de densidad ( f(x) ), entonces la esperanza matemática ( E(X) ) es:
( E(X) = int_{-infty}^{infty} x f(x) dx )
Conclusión
Como puedes ver, las aplicaciones de la integral definida son vastas y variadas. Desde la física y la ingeniería hasta la economía y las ciencias sociales, esta herramienta matemática es esencial para analizar y resolver problemas complejos. Espero que este artículo te haya proporcionado una visión general de cómo se utilizan las integrales definidas en diferentes campos y cómo pueden ser aplicadas en la vida real.
Si te interesa profundizar más en el tema, aquí te dejo algunos enlaces útiles:
