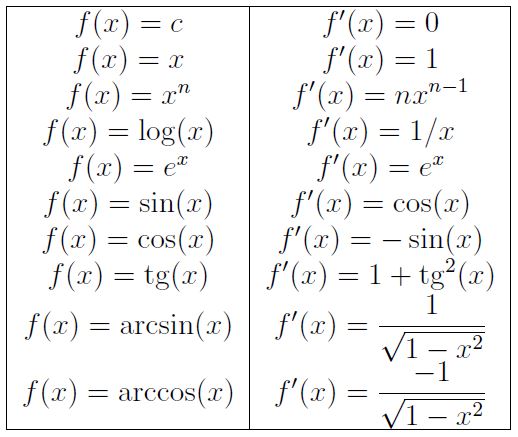
¡Hola! Soy Leandro y hoy vamos a sumergirnos en el fascinante mundo del cálculo diferencial. Puede que la palabra «cálculo» te remita a noches de insomnio y sudor frío, pero te prometo que, con la guía correcta, puede ser una experiencia reveladora y hasta emocionante. Así que, ¡vamos a ello!
¿Qué es el Cálculo Diferencial?
El cálculo diferencial es una rama de las matemáticas que se centra en el estudio de las tasas de cambio y las pendientes de las curvas. Dicho de manera sencilla, se trata de entender cómo cambian las cosas. Imagina que estás conduciendo un coche; el cálculo diferencial te ayuda a entender cómo varía tu velocidad en cada instante.
Historia del Cálculo Diferencial
El cálculo diferencial tiene una historia fascinante. Fue desarrollado de manera independiente por Isaac Newton y Gottfried Wilhelm Leibniz en el siglo XVII. Aunque ambos matemáticos tuvieron una acalorada disputa sobre quién fue el primero, hoy en día se les reconoce a ambos por su contribución fundamental a esta rama de la matemática.
Conceptos Básicos del Cálculo Diferencial
Para adentrarnos en el cálculo diferencial, primero necesitamos entender algunos conceptos básicos. Aquí te presento los más importantes:
Funciones
Una función es una relación entre dos conjuntos de números en la que a cada número del primer conjunto le corresponde exactamente un número del segundo conjunto. Por ejemplo, la función f(x) = 2x + 3 toma un número x y lo transforma en 2x + 3.
Derivadas
La derivada de una función es una medida de cómo cambia el valor de la función cuando cambia su entrada. Si tienes la función y = f(x), la derivada se denota como f'(x) o dy/dx. La derivada te dice la pendiente de la curva en cualquier punto, lo cual es increíblemente útil en una amplia variedad de aplicaciones.
Aplicaciones del Cálculo Diferencial
El cálculo diferencial no es solo un ejercicio académico; tiene aplicaciones prácticas en numerosos campos. Aquí te dejo algunos ejemplos:
Física
En física, el cálculo diferencial es fundamental para entender conceptos como la velocidad y la aceleración. La velocidad es la derivada de la posición con respecto al tiempo, y la aceleración es la derivada de la velocidad con respecto al tiempo. Sin el cálculo diferencial, muchas de las leyes de la física no tendrían sentido.
Ingeniería
La ingeniería utiliza el cálculo diferencial para diseñar y analizar sistemas complejos. Ya sea en la construcción de puentes, en el diseño de circuitos electrónicos o en la creación de software, el cálculo diferencial es una herramienta esencial.
Economía
En economía, el cálculo diferencial se usa para modelar y analizar el comportamiento de variables económicas. Por ejemplo, puede ayudar a entender cómo cambia la demanda de un producto cuando varía su precio.
Cómo Aprender Cálculo Diferencial
Aprender cálculo diferencial puede parecer intimidante al principio, pero hay muchos recursos disponibles para ayudarte. Aquí tienes algunos pasos que te recomiendo seguir:
Libros
Hay muchos libros excelentes sobre cálculo diferencial. Algunos de mis favoritos incluyen «Calculus» de James Stewart y «Calculus Made Easy» de Silvanus P. Thompson. Estos libros te guiarán paso a paso a través de los conceptos básicos y avanzados.
Cursos en Línea
Hay numerosos cursos en línea que te pueden enseñar cálculo diferencial. Plataformas como Coursera y Khan Academy ofrecen cursos gratuitos y de pago que son muy completos.
Práctica
Como con cualquier otra habilidad, la práctica es esencial. Resuelve tantos problemas como puedas y trata de entender cada paso del proceso. La práctica te ayudará a solidificar tus conocimientos y a ganar confianza.
Comparación con Otras Ramas del Cálculo
El cálculo diferencial es solo una parte del cálculo en general. También existe el cálculo integral, que se centra en la acumulación de cantidades. Mientras que el cálculo diferencial te dice cómo cambian las cosas, el cálculo integral te dice cuánto se acumula algo.
Cálculo Diferencial vs. Cálculo Integral
El cálculo diferencial y el integral están estrechamente relacionados. De hecho, el Teorema Fundamental del Cálculo establece que la diferenciación y la integración son procesos inversos. Así que, aunque son diferentes, ambos son igualmente importantes y útiles.
¿Cuál es más difícil?
Esta es una pregunta común y la respuesta depende del individuo. Algunas personas encuentran más intuitivo el cálculo diferencial porque se basa en el concepto de cambio, que es algo que experimentamos constantemente. Otras personas prefieren el cálculo integral porque les resulta más lógico pensar en la acumulación de cantidades. Lo importante es que ambos son esenciales y se complementan entre sí.
Recursos Adicionales
Aquí te dejo algunos recursos adicionales que te pueden ser útiles para aprender más sobre el cálculo diferencial:
- Math is Fun: Introduction to Differentiation
- Khan Academy: Calculus 1
- MIT OpenCourseWare: Single Variable Calculus
Conclusión
El cálculo diferencial es una herramienta poderosa que tiene aplicaciones en una amplia variedad de campos. Aunque puede parecer intimidante al principio, con la guía correcta y mucha práctica, puedes dominarlo. Espero que esta «Introducción al Cálculo Diferencial» te haya sido útil y te inspire a seguir explorando este fascinante tema. ¡Hasta la próxima!
