Introducción a las Propiedades de los Números
¡Hola! Soy Leandro y hoy vamos a sumergirnos en el maravilloso mundo de las propiedades de los números. Si alguna vez te has preguntado qué hace que un número sea especial o cómo podemos clasificarlos, estás en el lugar correcto. Desde números primos hasta irracionales, cada tipo tiene características únicas que los distinguen. Y, créeme, esto no es solo teoría; estas propiedades tienen aplicaciones prácticas en nuestra vida cotidiana y en la ciencia.
Los Números Primos y sus Propiedades
Los números primos son aquellos que solo tienen dos divisores: el 1 y ellos mismos. Esta característica los convierte en los «átomos» de la matemática, ya que cualquier número compuesto puede descomponerse en un producto de números primos. Por ejemplo, el número 15 se puede descomponer en 3 y 5. Fascinante, ¿verdad?
Importancia de los Números Primos
Los números primos no solo son curiosidades matemáticas, sino que también tienen aplicaciones prácticas en la criptografía, especialmente en la seguridad de datos. Por ejemplo, el algoritmo RSA, uno de los métodos de encriptación más utilizados, se basa en la dificultad de factorizar números grandes en sus factores primos.
Curiosidades sobre los Números Primos
Aquí va una curiosidad: no existe una fórmula simple para encontrar números primos, lo que los hace aún más intrigantes. Además, se ha demostrado que hay infinitos números primos, pero encontrar patrones entre ellos es una tarea extremadamente complicada.
Números Racionales: Propiedades y Ejemplos
Los números racionales son aquellos que pueden expresarse como el cociente de dos enteros, es decir, una fracción. Por ejemplo, 1/2 y 3/4 son números racionales. La característica principal de los números racionales es que tienen una representación decimal que es finita o periódica.
Aplicaciones de los Números Racionales
Los números racionales son esenciales en la vida cotidiana y en diversas aplicaciones científicas y económicas. Por ejemplo, cuando hablamos de tasas de interés, fracciones de segundos en cronometraje deportivo o proporciones en recetas de cocina, estamos utilizando números racionales.
Conversión de Números Racionales
La conversión de fracciones a decimales es una técnica útil que todos deberíamos dominar. Por ejemplo, 1/4 se convierte en 0.25 y 3/5 en 0.6. Esta habilidad es especialmente útil en cálculos rápidos y en la resolución de problemas matemáticos.
Números Irracionales: Propiedades y Ejemplos
Los números irracionales son aquellos que no pueden expresarse como el cociente de dos enteros. Esto significa que su representación decimal es infinita y no periódica. Ejemplos clásicos de números irracionales son π (pi) y √2 (la raíz cuadrada de 2).
Diferencias entre Números Racionales e Irracionales
La principal diferencia entre los números racionales e irracionales radica en su representación decimal. Mientras que los racionales tienen una representación decimal finita o periódica, los irracionales tienen una representación infinita y no periódica. Esta propiedad hace que los irracionales sean particularmente interesantes y, a veces, desafiantes de trabajar en matemáticas.
Importancia de los Números Irracionales
Los números irracionales tienen aplicaciones en diversas áreas de la ciencia y la ingeniería. Por ejemplo, π (pi) es fundamental en geometría y trigonometría, mientras que √2 es crucial en cálculos de geometría y álgebra.
Números Enteros: Propiedades y Usos Cotidianos
Los números enteros incluyen todos los números positivos, negativos y el cero. Son quizás los más familiares para nosotros, ya que los usamos a diario en conteos, balances y muchas otras situaciones comunes.
Propiedades de los Números Enteros
Los números enteros tienen varias propiedades interesantes, como la propiedad de clausura, la propiedad conmutativa, la asociativa y la distributiva. Estas propiedades facilitan las operaciones matemáticas básicas como la suma, resta, multiplicación y división.
Aplicaciones en la Vida Diaria
Desde llevar un balance de nuestras finanzas hasta contar los días en un calendario, los números enteros son una parte integral de nuestra vida diaria. Entender sus propiedades nos ayuda a realizar cálculos rápidos y precisos.
Números Reales y Complejos: Una Introducción
Los números reales comprenden tanto los números racionales como los irracionales. En otras palabras, cualquier número que pueda representarse en una recta numérica es un número real. Por otro lado, los números complejos incluyen una parte real y una parte imaginaria, y son fundamentales en campos avanzados de la ciencia y la ingeniería.
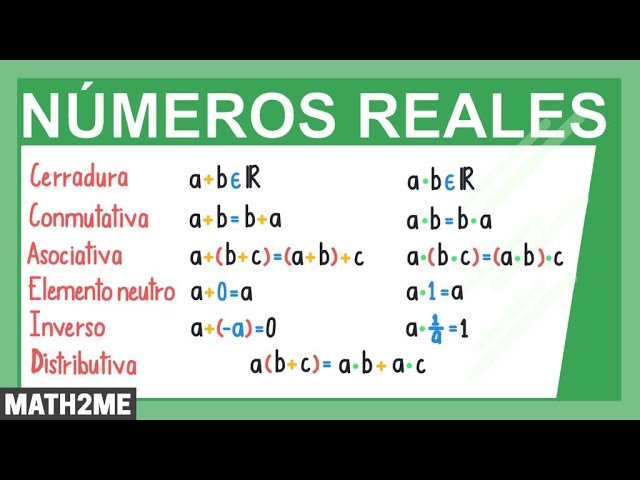
Propiedades de los Números Reales
Los números reales tienen propiedades como la densidad, lo que significa que entre dos números reales siempre hay otro número real. Esta propiedad es crucial en el análisis matemático y en la resolución de problemas de continuidad.
Propiedades de los Números Complejos
Los números complejos tienen propiedades únicas, como la capacidad de representar fenómenos que no pueden describirse con números reales, como las ondas electromagnéticas. La parte imaginaria de un número complejo se denota con la letra «i», que es la raíz cuadrada de -1.
Conexión entre Diferentes Tipos de Números
Uno de los aspectos más fascinantes de las propiedades de los números es cómo se interrelacionan. Por ejemplo, cualquier número entero es también un número racional (porque puede expresarse como una fracción con denominador 1), y cualquier número racional es un número real.
De Enteros a Racionales e Irracionales
Comprender estas conexiones nos ayuda a navegar mejor el mundo de las matemáticas. Saber que 5 es tanto un entero como un racional y un real nos permite utilizar este número en diferentes contextos matemáticos.
La Importancia de las Propiedades en Problemas Matemáticos
Conocer las propiedades de los diferentes tipos de números nos permite resolver problemas matemáticos de manera más eficiente. Por ejemplo, saber que los números irracionales no pueden ser expresados como fracciones nos ayuda a identificar soluciones incorrectas en problemas de raíces cuadradas y otras operaciones.
Conclusión: La Belleza de las Propiedades de los Números
En resumen, las propiedades de los números son esenciales para entender el vasto mundo de las matemáticas. Desde los números primos hasta los complejos, cada tipo de número tiene características únicas que los hacen especiales. Espero que esta exploración te haya ayudado a apreciar la belleza y utilidad de estas propiedades. ¡Hasta la próxima!
