Integrales: Todo lo que Necesitas Saber
Introducción a las Integrales
Hola, soy Leandro, y hoy vamos a sumergirnos en el fascinante mundo de las integrales. ¿Alguna vez has escuchado hablar de ellas y te has preguntado de qué rayos van? Bueno, déjame decirte que no estás solo. Las integrales son una de esas cosas que parecen intimidantes al principio, pero una vez que les agarras el truco, se vuelven increíblemente útiles y, me atrevo a decir, hasta divertidas.
En este artículo, vamos a explorar todo lo que necesitas saber sobre las integrales: qué son, por qué son importantes, y cómo se utilizan en diferentes campos. Así que prepárate para un viaje matemático que, espero, te dejará con ganas de saber más.
¿Qué Son las Integrales?
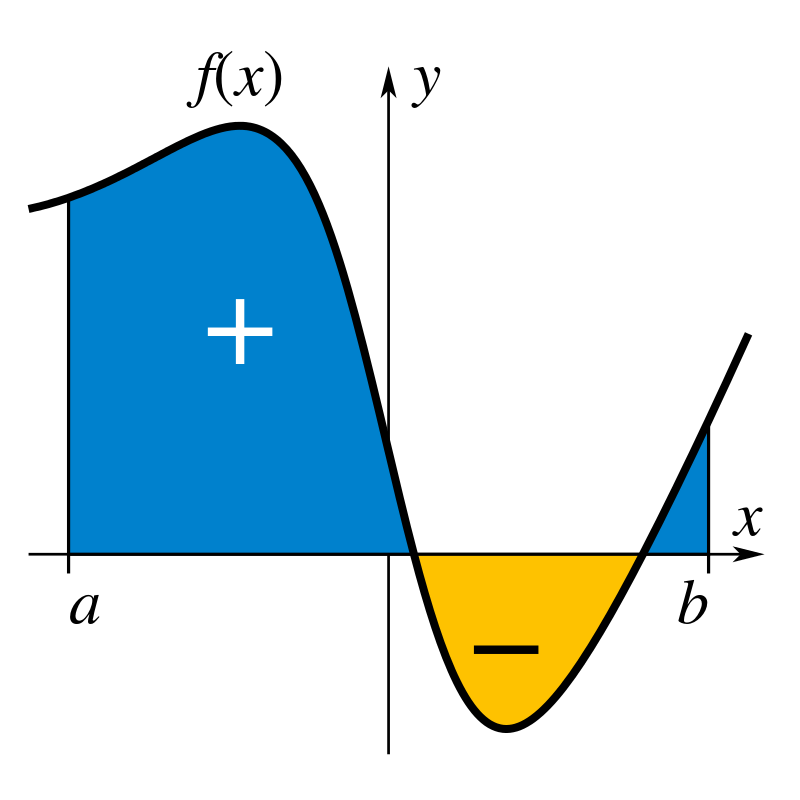
Para empezar, una integral es una operación matemática que nos permite encontrar el área bajo una curva. Imagina que tienes una función que describe una curva en un gráfico. La integral de esa función te da el área entre la curva y el eje x, desde un punto a hasta un punto b. Bastante chulo, ¿no?
En términos más formales, la integral de una función f(x) desde a hasta b se denota como:
∫ab f(x) dx
Donde ∫ es el símbolo de la integral, f(x) es la función, y dx indica que estamos integrando respecto a x.
Conceptos Básicos de las Integrales
Para entender las integrales, primero necesitamos hablar de su concepto hermano: la derivada. Si la derivada nos dice cómo cambia una función, la integral nos dice cuánto se acumula. Es como la diferencia entre la velocidad (derivada) y la distancia recorrida (integral).
La notación de una integral puede parecer intimidante al principio: ∫ f(x) dx. Pero no te preocupes, vamos a desglosarlo:
- ∫ es el símbolo de la integral.
- f(x) es la función que estamos integrando.
- dx indica que estamos integrando con respecto a x.
Tipos de Integrales
Integrales Definidas
Las integrales definidas son aquellas que tienen límites especificados, es decir, un punto de inicio y un punto de fin. Estas integrales se utilizan principalmente para calcular áreas y valores acumulados. Por ejemplo, si quieres encontrar el área bajo una curva entre x = 1 y x = 3, usarías una integral definida.
Integrales Indefinidas
Por otro lado, las integrales indefinidas no tienen límites de integración. En lugar de calcular un área específica, estas integrales te dan una familia de funciones antiderivadas. Básicamente, te dicen qué función derivada te da la función original. La notación para una integral indefinida es simplemente:
∫ f(x) dx = F(x) + C
Donde C es la constante de integración.
Integrales Impropias
Las integrales impropias son aquellas en las que uno o ambos límites de integración son infinitos, o la función tiene una discontinuidad en el intervalo de integración. Se utilizan para calcular áreas y volúmenes en casos donde la integral definida no puede aplicarse directamente.
Por ejemplo, ∫[1, ∞) 1/x^2 dx es una integral impropia, y su valor es 1.
Aplicaciones de las Integrales
Las integrales no son solo teoría matemática abstracta; tienen aplicaciones prácticas en diversos campos. Aquí te dejo algunos ejemplos:
Física
En física, las integrales se utilizan para calcular cantidades como el trabajo realizado por una fuerza, la cantidad de carga en un conductor, y el momento de inercia de un objeto. Por ejemplo, el trabajo realizado por una fuerza variable F(x) a lo largo de una distancia se calcula mediante la integral de F(x) respecto a x.
Otra aplicación importante es en el cálculo de centros de masa y momentos de inercia. Por ejemplo, el momento de inercia I de una masa m distribuida a lo largo de una distancia se calcula mediante la integral ∫ r^2 dm, donde r es la distancia al eje de rotación.
Economía
En economía, las integrales se utilizan para modelar y analizar el crecimiento económico, el costo total, y la función de demanda. Por ejemplo, el excedente del consumidor se calcula mediante la integral de la función de demanda.
Otra aplicación es en la determinación del valor presente neto (VPN) de una serie de flujos de caja futuros, utilizando la fórmula del valor presente, que involucra la integración de una función de flujo de caja descontada a una tasa de interés específica.
Ingeniería
En ingeniería, las integrales se aplican en el análisis de estructuras, la dinámica de fluidos, y el diseño de sistemas eléctricos. Las integrales nos permiten modelar y analizar sistemas complejos, como el flujo de corriente en un circuito o la distribución de tensiones en un puente.
Por ejemplo, en la dinámica de fluidos, la ecuación de continuidad y las ecuaciones de Navier-Stokes, que describen el comportamiento de los fluidos, utilizan integrales para modelar el flujo de fluidos y la conservación de masa y energía.
Cómo Resolver Integrales
Resolver integrales puede ser todo un desafío, pero no te preocupes, aquí te dejo algunos métodos y trucos que te pueden ayudar:
Integración por Sustitución
La integración por sustitución es una técnica que simplifica la integral haciendo un cambio de variable. Es especialmente útil cuando la integral es complicada y necesita ser transformada a una forma más sencilla.
Por ejemplo, para integrar ∫ x * cos(x^2) dx, podemos hacer la sustitución u = x^2, du = 2x dx. Esto transforma la integral en (1/2) ∫ cos(u) du, que es más fácil de resolver.
Integración por Partes
La integración por partes es otra técnica útil, especialmente cuando tienes un producto de funciones. La fórmula básica es:
∫ u dv = uv - ∫ v du
Donde u y v son funciones de x.
Integración Numérica
- Método del Trapecio: Aproxima el área bajo la curva dividiéndola en una serie de trapecios.
- Método de Simpson: Utiliza parábolas para aproximar el área bajo la curva, proporcionando una aproximación más precisa que el método del trapecio.
Tablas de Integrales
Finalmente, no subestimes el poder de las tablas de integrales. Estas tablas contienen una lista de integrales comunes y sus soluciones, y pueden ser un salvavidas cuando te encuentras con una integral complicada.
Recursos Adicionales
Si quieres profundizar aún más en el tema de las integrales, aquí te dejo algunos enlaces y recursos que te pueden resultar útiles:
- Khan Academy: Ofrece una serie de videos y ejercicios interactivos que explican las integrales de una manera accesible para principiantes. Khan Academy
- Wolfram Alpha: Un motor de cálculo que puede resolver integrales simbólicas y numéricas, proporcionando pasos detallados y gráficos. Wolfram Alpha
- MathWorld: Un recurso enciclopédico que ofrece definiciones formales y ejemplos detallados de integrales. MathWorld
- YouTube Channels (3Blue1Brown, Mathologer): Estos canales explican conceptos de cálculo, incluyendo integrales, usando animaciones visualmente atractivas y ejemplos prácticos. 3Blue1Brown
Ejemplos Prácticos de Integrales
Cálculo de Áreas con Integrales
Supongamos que queremos calcular el área bajo la curva y = x^3 entre x = 0 y x = 2. La integral definida es:
∫[0, 2] x^3 dx = [1/4 * x^4] (evaluado de 0 a 2) = 1/4 * 2^4 – 1/4 * 0^4 = 4.
Así, el área bajo la curva es 4 unidades cuadradas.
Cálculo de Volúmenes con Integrales
Podemos usar integrales para calcular el volumen de sólidos de revolución. Por ejemplo, para encontrar el volumen del sólido formado al girar y = √x alrededor del eje x desde x = 0 hasta x = 1, usamos la fórmula del volumen de revolución:
V = π ∫[0, 1] (√x)^2 dx = π ∫[0, 1] x dx = π [1/2 * x^2] (evaluado de 0 a 1) = π/2.
El volumen del sólido es π/2 unidades cúbicas.
Aplicaciones de Integrales en Economía
Supongamos que una empresa tiene una función de costos marginales C'(x) = 5 + 0.01x, donde x es el número de unidades producidas. Para encontrar el costo total de producir 100 unidades, integramos la función de costos marginales:
C(x) = ∫ (5 + 0.01x) dx = 5x + 0.01/2 * x^2 + C.
Evaluando de 0 a 100, obtenemos:
C(100) = 5*100 + 0.01/2 * 100^2 = 500 + 50 = 550.
Así, el costo total de producir 100 unidades es 550.
Conclusión sobre Integrales
Las integrales son una herramienta poderosa y versátil en el arsenal de cualquier matemático, científico o ingeniero. Desde calcular áreas y volúmenes hasta resolver problemas complejos en física y economía, las integrales nos permiten comprender y modelar el mundo de maneras profundas y precisas.
Espero que este artículo te haya dado una visión clara y accesible de lo que son las integrales y cómo se utilizan. Recuerda, la clave para dominar las integrales es practicar, practicar y practicar. Así que no te desanimes si al principio parece complicado. Con el tiempo y la experiencia, verás que las integrales no son tan intimidantes como parecen.
¡Gracias por acompañarme en esta aventura matemática! Si tienes alguna pregunta o quieres saber más sobre algún tema específico, no dudes en dejar un comentario. ¡Hasta la próxima!
