Derivadas: Todo lo que Necesitas Saber
¿Qué son las Derivadas?
Hola, soy Leandro, un apasionado de las matemáticas y hoy quiero hablarte sobre un tema que puede parecer complicado al principio, pero que en realidad es fascinante: las derivadas. ¿Qué son exactamente? Bueno, en términos simples, una derivada mide cómo cambia una función conforme cambian sus variables. Si alguna vez has escuchado términos como «tasa de cambio» o «pendiente de una curva», estás hablando de derivadas.
Historia y Origen de las Derivadas
Las derivadas tienen una historia rica y fascinante. Fueron desarrolladas en el siglo XVII por dos de los matemáticos más famosos de todos los tiempos: Isaac Newton y Gottfried Wilhelm Leibniz. Aunque ambos llegaron a conceptos similares de forma independiente, sus notaciones y enfoques eran diferentes. La disputa entre Newton y Leibniz sobre quién fue el verdadero inventor del cálculo diferencial (que incluye las derivadas) es una de las más famosas en la historia de las matemáticas.
Definición Formal de Derivada
Para los más técnicos y puristas, la definición formal de una derivada es la siguiente: la derivada de una función f(x) en un punto a es el límite de la tasa de cambio promedio de la función conforme el intervalo se reduce a cero. Matemáticamente, esto se expresa como:
[ f'(a) = lim_{{h to 0}} frac{f(a+h) – f(a)}{h} ]
Esta fórmula puede parecer intimidante, pero todo se reduce a calcular la pendiente de la tangente a la curva en un punto específico.
Aplicaciones de las Derivadas
Las derivadas no solo son una curiosidad matemática; tienen aplicaciones prácticas en diversas áreas. Algunas de las aplicaciones más comunes incluyen:
1. Física
En física, las derivadas se utilizan para describir el movimiento. Por ejemplo, la velocidad es la derivada de la posición respecto al tiempo, y la aceleración es la derivada de la velocidad.
2. Economía
En economía, las derivadas se usan para encontrar tasas de cambio, como la tasa de crecimiento del producto interno bruto (PIB) o la elasticidad de la demanda.
3. Ingeniería
En ingeniería, las derivadas se utilizan para modelar y analizar sistemas dinámicos, desde el control de procesos hasta el diseño de estructuras.
4. Biología
En biología, las derivadas se aplican para estudiar el crecimiento de poblaciones, la difusión de sustancias y muchos otros fenómenos naturales.
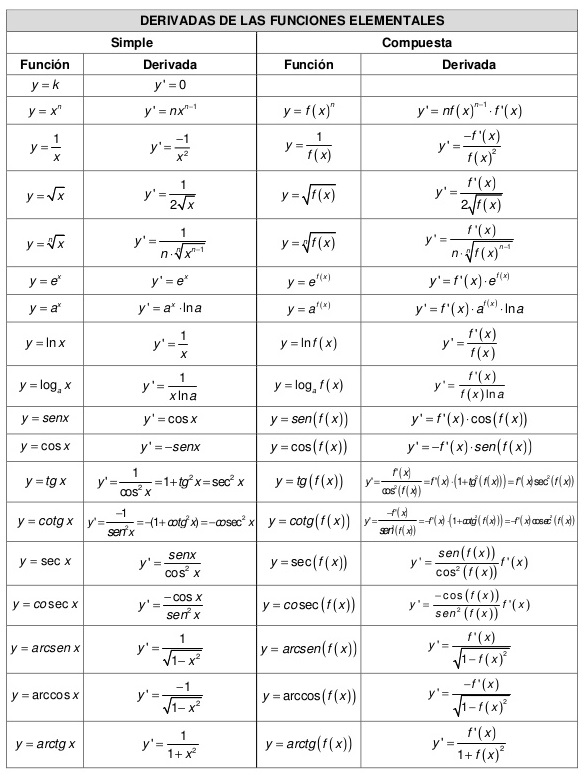
Reglas de Derivación
Dominar las derivadas implica familiarizarse con varias reglas de derivación. Aquí te presento algunas de las más importantes:
1. Regla del Poder
Si tienes una función de la forma f(x) = x^n, entonces su derivada es f'(x) = nx^{(n-1)}.
2. Regla del Producto
Si tienes dos funciones u(x) y v(x), la derivada de su producto es u'(x)v(x) + u(x)v'(x).
3. Regla del Cociente
Si tienes dos funciones u(x) y v(x), la derivada de su cociente es ( frac{u'(x)v(x) – u(x)v'(x)}{[v(x)]^2} ).
4. Regla de la Cadena
Si tienes una función compuesta f(g(x)), su derivada es f'(g(x)) cdot g'(x).
Ejemplos Prácticos de Derivadas
Vamos a ver algunos ejemplos prácticos para entender mejor todo esto:
1. Ejemplo con la Regla del Poder
Supongamos que f(x) = x^3. Utilizando la regla del poder, sabemos que f'(x) = 3x^2.
2. Ejemplo con la Regla del Producto
Supongamos que u(x) = x^2 y v(x) = sin(x). Entonces, la derivada de u(x)v(x) es 2x cdot sin(x) + x^2 cdot cos(x).
3. Ejemplo con la Regla del Cociente
Supongamos que u(x) = x^2 y v(x) = cos(x). Entonces, la derivada de ( frac{u(x)}{v(x)} ) es ( frac{2x cdot cos(x) – x^2 cdot (-sin(x))}{(cos(x))^2} ).
4. Ejemplo con la Regla de la Cadena
Supongamos que f(x) = sin(x^2). Entonces, la derivada es 2x cdot cos(x^2).
Derivadas de Funciones Trigonométricas
Las funciones trigonométricas también tienen sus propias derivadas. Aquí te dejo algunas de las más comunes:
- La derivada de sin(x) es cos(x).
- La derivada de cos(x) es – sin(x).
- La derivada de tan(x) es sec^2(x).
- La derivada de cot(x) es -csc^2(x).
- La derivada de sec(x) es sec(x) cdot tan(x).
- La derivada de csc(x) es -csc(x) cdot cot(x).
Derivadas Implícitas
En algunos casos, las funciones no están dadas de forma explícita. En estos casos, necesitamos usar la derivación implícita. Por ejemplo, si tenemos una ecuación de la forma x^2 + y^2 = 1, podemos derivar ambos lados con respecto a x para obtener 2x + 2y(dy/dx) = 0. Resolviendo para dy/dx, obtenemos dy/dx = -x/y.
Segundas Derivadas y Más Allá
No solo podemos calcular la primera derivada de una función, también podemos calcular la segunda derivada, la tercera derivada, y así sucesivamente. La segunda derivada mide la tasa de cambio de la tasa de cambio, y es útil para entender la concavidad de una función. Por ejemplo, si f(x) = x^3, entonces f'(x) = 3x^2 y f»(x) = 6x.
Recursos Adicionales sobre Derivadas
Si deseas profundizar más en el tema de las derivadas, aquí tienes algunos enlaces útiles:
Conclusión
Espero que esta introducción a las derivadas te haya sido útil. Como has visto, las derivadas son una herramienta poderosa en matemáticas y tienen aplicaciones en muchos campos. Si bien pueden parecer complicadas al principio, con un poco de práctica y paciencia, puedes dominarlas. ¡Hasta la próxima!
