Introducción a las funciones y gráficos

Hola, soy Leandro, y hoy vamos a sumergirnos en un tema fundamental tanto en matemáticas como en muchas otras disciplinas: las funciones y gráficos. A lo largo de mi carrera, he tenido la oportunidad de trabajar con ellos de manera intensa, y puedo decirte que entender su relación y diferencias puede abrirte un mundo de posibilidades.

Las funciones y gráficos son pilares esenciales en el estudio de las matemáticas, y su aplicación se extiende a la física, la economía, la informática, entre otras áreas. Desde la representación de datos hasta la resolución de ecuaciones complejas, su utilidad es innegable. Así que, sin más preámbulos, vamos a explorarlos con profundidad.

¿Qué es una función?

Definición y conceptos básicos

En términos simples, una función es una relación entre dos conjuntos: un conjunto de entrada (dominio) y un conjunto de salida (codominio). Cada elemento del dominio está relacionado con un único elemento del codominio. Matemáticamente, una función se denota como f(x), donde x es el valor de entrada y f(x) es el valor de salida.

Tipos de funciones

Hay varios tipos de funciones que podemos encontrar, cada una con sus propias características y aplicaciones:

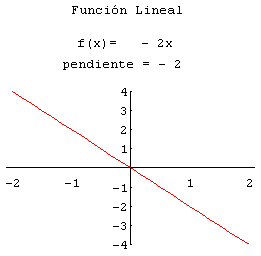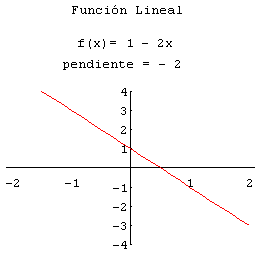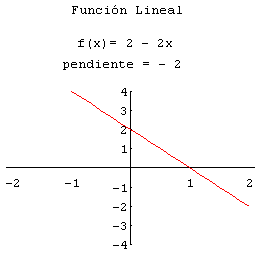
• Funciones lineales: Tienen la forma f(x) = mx + b. Son las más básicas y representan líneas rectas en un gráfico.
• Funciones cuadráticas: Tienen la forma f(x) = ax² + bx + c. Estas funciones forman parábolas.
• Funciones exponenciales: Tienen la forma f(x) = a^x. Son cruciales en el estudio del crecimiento y decaimiento exponencial.
• Funciones logarítmicas: Son la inversa de las funciones exponenciales y son vitales en muchos campos científicos.

¿Qué es un gráfico?

Definición y conceptos básicos

Un gráfico es una representación visual de datos o de una función. En el contexto de las matemáticas, un gráfico de una función es una manera de mostrar cómo los valores de entrada (x) se relacionan con los valores de salida (f(x)). Los gráficos nos permiten visualizar las propiedades y el comportamiento de una función de manera intuitiva.

Tipos de gráficos

Existen diversos tipos de gráficos utilizados para representar funciones y datos:

• Gráficos de líneas: Son ideales para mostrar la relación entre dos variables continuas.
• Gráficos de barras: Se usan para comparar diferentes categorías.
• Gráficos de dispersión: Son útiles para observar la relación entre dos variables cuantitativas.
• Gráficos de pastel: Perfectos para mostrar proporciones y porcentajes.

Relación entre funciones y gráficos

Cómo se representan las funciones en los gráficos

La representación gráfica de una función nos permite comprender mejor su comportamiento. Por ejemplo, la gráfica de una función lineal es una línea recta, mientras que la gráfica de una función cuadrática es una parábola. Para representar una función en un gráfico, simplemente trazamos puntos que correspondan a los pares (x, f(x)) y los conectamos.

Ejemplos prácticos

Vamos a ver algunos ejemplos para entender mejor cómo se representan las funciones en los gráficos:

• Función lineal: Si tenemos la función f(x) = 2x + 3, su gráfica es una línea recta que cruza el eje y en 3 y tiene una pendiente de 2.
• Función cuadrática: Para la función f(x) = x² – 4x + 4, la gráfica es una parábola que se abre hacia arriba y tiene su vértice en (2, 0).
• Función exponencial: La función f(x) = 2^x tiene una gráfica que crece rápidamente a medida que x aumenta.

Diferencias entre funciones y gráficos

Conceptuales y prácticas

Es crucial entender las diferencias entre funciones y gráficos, tanto en el aspecto conceptual como en el práctico. Mientras que las funciones son relaciones matemáticas abstractas entre dos conjuntos, los gráficos son representaciones visuales de esas relaciones.

Ventajas y desventajas

Ambos, funciones y gráficos, tienen sus propias ventajas y desventajas:

• Funciones: Son exactas y permiten realizar cálculos precisos. Sin embargo, pueden ser difíciles de interpretar sin una representación visual.
• Gráficos: Facilitan la comprensión intuitiva y visual de los datos, pero pueden perder precisión y no siempre muestran todos los detalles.

Aplicaciones prácticas de funciones y gráficos

En diferentes disciplinas

Las aplicaciones de funciones y gráficos son vastas y variadas, abarcando múltiples disciplinas:

• Matemáticas: Desde el álgebra hasta el cálculo, las funciones y gráficos son esenciales para entender conceptos matemáticos.
• Economía: Las funciones y gráficos se usan para modelar el comportamiento del mercado y predecir tendencias económicas.
• Física: Permiten modelar fenómenos físicos y entender relaciones entre variables como velocidad, aceleración y tiempo.
• Informática: Son cruciales para el análisis de algoritmos y la visualización de datos.

Conclusión

En resumen, las funciones y gráficos son componentes fundamentales en el estudio de las matemáticas y muchas otras disciplinas. Mientras que las funciones nos proporcionan una manera precisa de describir relaciones matemáticas, los gráficos nos ofrecen una representación visual que facilita la comprensión y el análisis. La combinación de ambos nos permite explorar y entender el mundo de una manera más completa y efectiva.