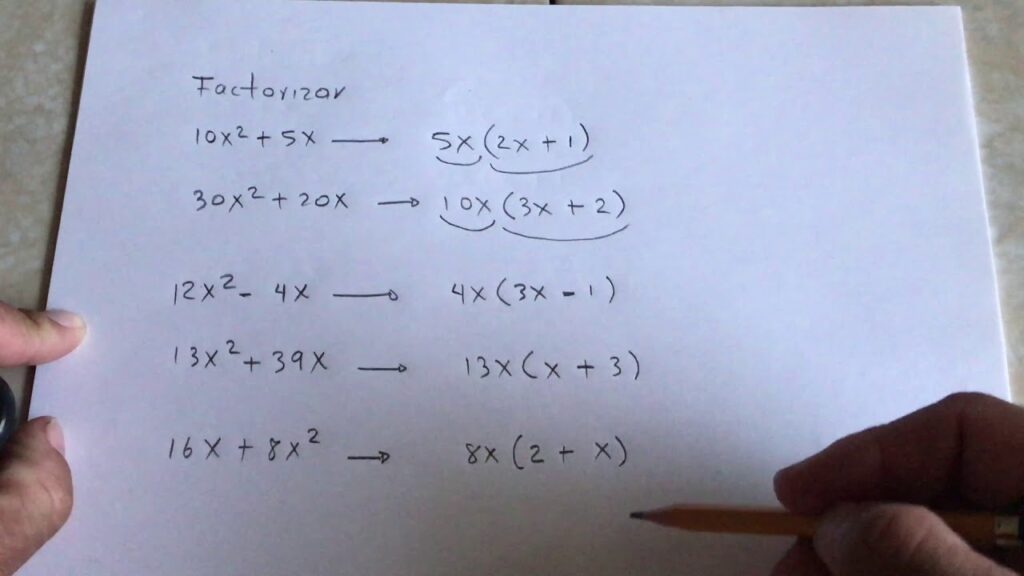
Todo lo que Necesitas Saber
Introducción a la Factorización de Expresiones Algebraicas
¡Hola! Soy Leandro y hoy vamos a sumergirnos en el fascinante mundo de la factorización de expresiones algebraicas. Si alguna vez te has preguntado qué es, por qué es importante o cómo se hace, estás en el lugar correcto. Llevo años dedicándome a las matemáticas y puedo asegurarte que dominar esta técnica te abrirá muchas puertas en el campo del álgebra.
¿Qué es la Factorización de Expresiones Algebraicas?
La factorización es una herramienta algebraica que consiste en descomponer una expresión en productos de otras expresiones más simples. Imagina que tienes un número como 12. Puedes descomponerlo en factores primos: 2 x 2 x 3. De manera similar, en el álgebra, factorizar significa reescribir una expresión en términos de productos de factores más simples.
Importancia de la Factorización en Álgebra
La factorización en álgebra no es solo un ejercicio académico; tiene aplicaciones prácticas en la resolución de ecuaciones, simplificación de expresiones y en el cálculo integral y diferencial. La capacidad de factorizar correctamente puede simplificar enormemente problemas complejos y hacer que las soluciones sean más accesibles.
Métodos de Factorización de Expresiones Algebraicas
Existen varios métodos para factorizar expresiones algebraicas. Aquí te explico algunos de los más comunes:
Factor Común
Es el método más básico y consiste en extraer el mayor factor común de todos los términos de la expresión. Por ejemplo, en la expresión 6x + 9, el mayor factor común es 3, por lo que se puede reescribir como 3(2x + 3).
Factorización por Agrupación
Este método es útil cuando la expresión tiene cuatro términos o más. Consiste en agrupar los términos en pares y factorizar cada par por separado. Luego, se busca un factor común en los grupos resultantes. Por ejemplo, en la expresión ax + ay + bx + by, se puede agrupar como a(x + y) + b(x + y) y luego factorizar como (a + b)(x + y).
Factorización de Trinomios
Los trinomios de la forma ax² + bx + c se pueden factorizar buscando dos números que multiplicados den ac y sumados den b. Por ejemplo, para factorizar x² + 5x + 6, buscamos dos números que multiplicados den 6 y sumados den 5. Estos números son 2 y 3, por lo que la factorización es (x + 2)(x + 3).
Factorización de Diferencia de Cuadrados
Una diferencia de cuadrados se factoriza como el producto de una suma y una resta. Por ejemplo, a² – b² se factoriza como (a + b)(a – b). Este método es especialmente útil en la resolución de ecuaciones cuadráticas.
Aplicaciones Prácticas de la Factorización
La factorización de expresiones algebraicas tiene múltiples aplicaciones prácticas. Aquí te dejo algunas:
Resolución de Ecuaciones
Factorizar una ecuación puede simplificar enormemente su resolución. Por ejemplo, una ecuación cuadrática como x² – 5x + 6 = 0 se puede factorizar como (x – 2)(x – 3) = 0, lo que facilita encontrar las soluciones x = 2 y x = 3.
Simplificación de Expresiones
La factorización permite simplificar expresiones complejas, lo que facilita su manipulación y análisis. Por ejemplo, una fracción algebraica como (x² – 4)/(x – 2) se puede simplificar factorizando el numerador: (x + 2)(x – 2)/(x – 2), lo que resulta en x + 2 (asumiendo que x ≠ 2).
Cálculo Integral y Diferencial
En cálculo integral y diferencial, la factorización puede facilitar el proceso de integración y diferenciación. Por ejemplo, una integral como ∫(x² – 4)dx se puede simplificar factorizando el integrando: ∫(x + 2)(x – 2)dx, lo que permite aplicar técnicas de integración más fácilmente.
Recursos Adicionales y Enlaces de Interés
Si quieres profundizar más en el tema de la factorización de expresiones algebraicas, aquí te dejo algunos recursos útiles:
Conclusión
La factorización de expresiones algebraicas es una herramienta poderosa que puede simplificar muchos aspectos del álgebra y las matemáticas en general. Desde la resolución de ecuaciones hasta la simplificación de expresiones y el cálculo integral y diferencial, la factorización es una habilidad esencial que todos los estudiantes de matemáticas deberían dominar. Espero que este artículo te haya sido útil y te animo a seguir practicando y explorando este fascinante tema. ¡Hasta la próxima!
