Ecuaciones y Desigualdades – Guía Completa
¡Hola a todos! Soy Leandro, y hoy vamos a sumergirnos en el apasionante mundo de las ecuaciones y desigualdades. A lo largo de mi carrera, he tenido numerosas oportunidades de estudiar, enseñar y aplicar estos conceptos, y quiero compartir con ustedes todo lo que sé. Así que prepárense para una aventura matemática con un toque desenfadado pero lleno de autoridad. ¡Vamos allá!
¿Qué son las Ecuaciones?
Las ecuaciones son expresiones matemáticas en las que dos términos son iguales. Es decir, se establece una relación de igualdad entre dos expresiones algebraicas. Por ejemplo, la ecuación más sencilla y conocida es x + 5 = 10. En este caso, estamos buscando el valor de x que hace que la igualdad sea verdadera.
Tipos de Ecuaciones
Existen varios tipos de ecuaciones, cada una con sus características y métodos de resolución. Vamos a ver las más comunes:
Ecuaciones Lineales
Las ecuaciones lineales son aquellas en las que la variable tiene un exponente de uno. En otras palabras, son ecuaciones de primer grado. Un ejemplo es 2x + 3 = 7. Estas ecuaciones son las más sencillas de resolver y se pueden abordar con métodos básicos como el despeje de variables.
Ecuaciones Cuadráticas
Las ecuaciones cuadráticas son aquellas en las que la variable tiene un exponente de dos. Un ejemplo es x2 – 5x + 6 = 0. Estas ecuaciones suelen tener dos soluciones y se pueden resolver mediante factorización, completando el cuadrado o usando la fórmula cuadrática.
Ecuaciones Polinómicas
Las ecuaciones polinómicas involucran términos con exponentes enteros positivos. Por ejemplo, x3 – 2x2 + x – 1 = 0. La resolución de estas ecuaciones puede ser más compleja y a menudo requiere técnicas avanzadas o el uso de software matemático.
Ecuaciones Diferenciales
Las ecuaciones diferenciales son ecuaciones que involucran derivadas de una función. Estas ecuaciones son fundamentales en el estudio del cálculo y tienen aplicaciones en diversas áreas como la física y la ingeniería.
¿Qué son las Desigualdades?
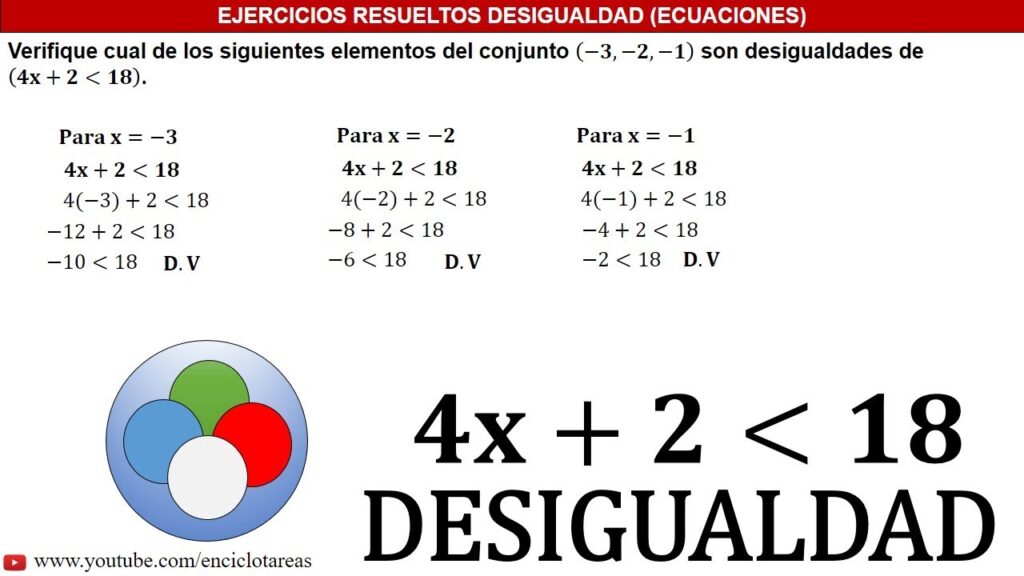
Las desigualdades, por otro lado, son expresiones matemáticas en las que una expresión no es necesariamente igual a otra, sino que puede ser mayor o menor. Por ejemplo, x + 3 < 7 es una desigualdad que establece que x más tres es menor que siete.
Tipos de Desigualdades
Al igual que las ecuaciones, las desigualdades también vienen en diferentes tipos y formas. Vamos a explorarlas:
Desigualdades Lineales
Las desigualdades lineales son aquellas en las que la variable tiene un exponente de uno. Un ejemplo es 2x + 3 > 5. Estas desigualdades son bastante directas y se pueden resolver de manera similar a las ecuaciones lineales.
Desigualdades Cuadráticas
Las desigualdades cuadráticas son aquellas en las que la variable tiene un exponente de dos. Por ejemplo, x2 – 4x + 3 < 0. La resolución de estas desigualdades puede implicar la factorización del polinomio y el análisis de los intervalos en los que la desigualdad es verdadera.
Desigualdades Racionales
Las desigualdades racionales implican fracciones en las que el numerador y/o el denominador son polinomios. Por ejemplo, (x + 1) / (x – 2) < 3. Resolver estas desigualdades puede ser más complejo y a menudo requiere un análisis cuidadoso de los puntos críticos y los signos de las expresiones en los intervalos.
Diferencias entre Ecuaciones y Desigualdades
Una de las preguntas más comunes que recibo es: «¿Cuál es la diferencia entre ecuaciones y desigualdades?» La diferencia principal radica en la relación establecida entre las expresiones algebraicas. Mientras que las ecuaciones establecen una igualdad, las desigualdades establecen una relación de mayor o menor entre las expresiones.
Soluciones Únicas vs. Conjuntos de Soluciones
En una ecuación, generalmente buscamos una solución única o un conjunto finito de soluciones que hacen que la igualdad sea verdadera. En cambio, en una desigualdad, estamos buscando un rango o intervalo de valores que satisfacen la relación de desigualdad.
Representación Gráfica
Las ecuaciones suelen representarse en un sistema de coordenadas como una línea o una curva. En contraste, las desigualdades se representan como regiones en el plano, indicando todas las posibles soluciones que cumplen la condición de desigualdad.
¿Cuál es Mejor: Ecuaciones o Desigualdades?
Esta es otra pregunta que surge con frecuencia: «¿Es mejor trabajar con ecuaciones o desigualdades?» La respuesta depende del contexto y de lo que se esté tratando de resolver. Las ecuaciones son ideales cuando buscamos soluciones precisas y definidas, mientras que las desigualdades son más útiles cuando necesitamos considerar un rango de valores posibles.
Aplicaciones de las Ecuaciones
Las ecuaciones son fundamentales en áreas como la física, la ingeniería y la economía. Nos permiten modelar situaciones reales y encontrar soluciones exactas a problemas específicos. Por ejemplo, las ecuaciones de movimiento en física nos ayudan a entender cómo se comportan los objetos bajo la influencia de fuerzas.
Aplicaciones de las Desigualdades
Las desigualdades, por otro lado, son extremadamente útiles en la optimización y la toma de decisiones. En economía, por ejemplo, se utilizan para definir restricciones y encontrar soluciones óptimas dentro de un conjunto de posibilidades. También son cruciales en el análisis de riesgo y en la teoría de juegos.
Cómo Resolver Ecuaciones y Desigualdades
¡Vamos a lo práctico! Resolver ecuaciones y desigualdades puede parecer intimidante al principio, pero con las técnicas adecuadas, se puede hacer de manera eficiente. A continuación, algunos métodos y estrategias para abordar estos problemas.
Resolución de Ecuaciones
La resolución de ecuaciones implica encontrar el valor de la variable que hace que la igualdad sea verdadera. Aquí algunos métodos comunes:
Despeje de Variables
Este es el método más básico y se utiliza principalmente en ecuaciones lineales. Consiste en aislar la variable en un lado de la ecuación. Por ejemplo, para resolver 2x + 3 = 7, restamos 3 de ambos lados y luego dividimos por 2.
Factorización
En el caso de ecuaciones cuadráticas, la factorización puede ser una herramienta poderosa. Por ejemplo, para resolver x2 – 5x + 6 = 0, podemos factorizarlo como (x – 2)(x – 3) = 0 y luego resolver para x.
Fórmula Cuadrática
Cuando la factorización no es posible, la fórmula cuadrática x = (-b ± √(b2 – 4ac)) / 2a es una solución universal para las ecuaciones cuadráticas.
Resolución de Desigualdades
La resolución de desigualdades implica encontrar el rango de valores que hacen que la desigualdad sea verdadera. Aquí algunos métodos comunes:
Despeje de Variables
Al igual que con las ecuaciones, el despeje de variables es un método básico. Sin embargo, debemos tener en cuenta que al multiplicar o dividir por un número negativo, la dirección de la desigualdad cambia.
Intervalos y Análisis de Signos
En el caso de desigualdades cuadráticas o racionales, a menudo es útil analizar los intervalos. Esto implica encontrar los puntos críticos y determinar en qué intervalos la desigualdad es verdadera.
Recursos Adicionales y Enlaces Relacionados
Si desean profundizar más en el tema de ecuaciones y desigualdades, aquí algunos recursos útiles:
- Khan Academy – Álgebra
- Khan Academy – Desigualdades
- Coursera – Introduction to Algebra
- edX – Introduction to Algebra
Competencia en el Nicho
Existen muchos artículos y recursos que abordan el tema de ecuaciones y desigualdades. Algunos sitios de referencia incluyen:
Estos sitios ofrecen una variedad de artículos, tutoriales y recursos educativos que pueden ser muy útiles para complementar lo que hemos discutido aquí.
Conclusión
Espero que hayan disfrutado de esta exploración sobre las ecuaciones y desigualdades. Hemos cubierto desde los conceptos básicos hasta las aplicaciones más avanzadas y las técnicas de resolución. Recuerden, la práctica hace al maestro, así que no duden en seguir practicando y explorando estos fascinantes temas matemáticos.
¡Hasta la próxima, y sigan resolviendo!
