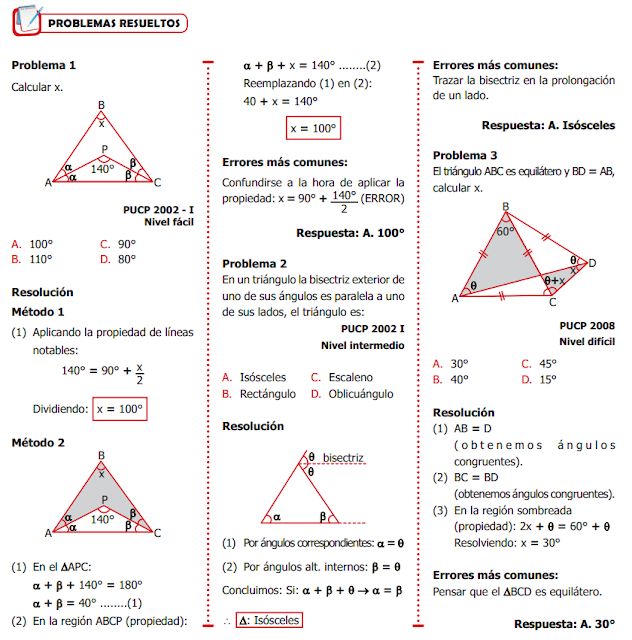
Ejemplos de Problemas de Geometría
Introducción a los Problemas de Geometría
¡Hola a todos! Mi nombre es Leandro y hoy quiero compartir con ustedes mi experiencia y conocimientos sobre los problemas de geometría. A lo largo de los años he tenido la oportunidad de resolver una amplia variedad de problemas geométricos y me he dado cuenta de que muchas personas encuentran este tema desafiante. En este artículo, exploraremos diferentes ejemplos de problemas de geometría y aprenderemos a resolverlos de manera efectiva.
Tipos Comunes de Problemas de Geometría
La geometría es una rama de las matemáticas que se ocupa de las propiedades y relaciones de los puntos, líneas, superficies y sólidos. Los problemas de geometría pueden variar desde simples cálculos de área y perímetro hasta complejas demostraciones geométricas. A continuación, vamos a revisar algunos de los tipos más comunes de problemas geométricos:
Problemas de Área y Perímetro
Uno de los tipos más básicos de problemas de geometría son aquellos que implican cálculos de área y perímetro. Estos problemas suelen ser los primeros que los estudiantes encuentran en sus estudios de geometría. Por ejemplo, calcular el área de un triángulo, un cuadrado o un círculo. La clave para resolver estos problemas es conocer las fórmulas adecuadas y aplicarlas correctamente.
Problemas de Volumen y Superficie
Otro tipo común de problemas geométricos son aquellos que implican el cálculo de volúmenes y superficies de sólidos. Estos problemas son un poco más avanzados y requieren una comprensión de las fórmulas para figuras tridimensionales como cilindros, esferas y prismas.
Problemas de Triángulos
Los triángulos son una figura geométrica fundamental y hay una gran cantidad de problemas que involucran triángulos. Estos problemas pueden incluir la aplicación del teorema de Pitágoras, la ley de senos y cosenos, y la resolución de triángulos utilizando trigonometría.
Problemas de Coordenadas
Los problemas de geometría coordenada implican el uso de un sistema de coordenadas para describir ubicaciones y resolver problemas. Estos problemas pueden incluir la determinación de la distancia entre dos puntos, la ecuación de una recta o el área de una figura en el plano cartesiano.
Ejemplos de Problemas de Geometría y Cómo Resolverlos
Ahora que hemos revisado algunos de los tipos más comunes de problemas geométricos, vamos a ver algunos ejemplos específicos y cómo resolverlos paso a paso.
Ejemplo 1: Calcular el Área de un Triángulo
Problema: Calcular el área de un triángulo con una base de 10 cm y una altura de 5 cm.
Solución: La fórmula para calcular el área de un triángulo es Área = 1/2 × base × altura. Sustituimos los valores dados:
Área = 1/2 × 10 cm × 5 cm = 25 cm²
Por lo tanto, el área del triángulo es 25 cm².
Ejemplo 2: Calcular el Volumen de un Cilindro
Problema: Calcular el volumen de un cilindro con un radio de 3 cm y una altura de 7 cm.
Solución: La fórmula para calcular el volumen de un cilindro es Volumen = π × radio² × altura. Sustituimos los valores dados:
Volumen = π × (3 cm)² × 7 cm = π × 9 cm² × 7 cm ≈ 198.94 cm³
Por lo tanto, el volumen del cilindro es aproximadamente 198.94 cm³.
Ejemplo 3: Teorema de Pitágoras
Problema: En un triángulo rectángulo, los catetos miden 6 cm y 8 cm. Calcular la longitud de la hipotenusa.
Solución: Según el teorema de Pitágoras, en un triángulo rectángulo, la hipotenusa al cuadrado es igual a la suma de los cuadrados de los catetos. Es decir, a² + b² = c². Sustituimos los valores dados:
(6 cm)² + (8 cm)² = c²
36 cm² + 64 cm² = c²
100 cm² = c²
c = √100 cm² = 10 cm
Por lo tanto, la longitud de la hipotenusa es 10 cm.
Recursos Adicionales y Enlaces Relacionados
Para aquellos que desean profundizar aún más en la resolución de problemas geométricos, aquí hay algunos recursos adicionales y enlaces relacionados que pueden ser de gran ayuda:
Conclusión
La geometría es una disciplina fascinante que nos permite comprender mejor el mundo que nos rodea. A través de la práctica y el estudio constante, podemos resolver problemas geométricos con mayor facilidad y precisión. Espero que este artículo les haya proporcionado una visión clara y útil de los diferentes tipos de problemas geométricos y cómo abordarlos. ¡Hasta la próxima!
