Hola, soy Leandro y hoy vamos a embarcarnos en un viaje fascinante por el mundo de los números irracionales. Este es un tema que puede parecer complejo, pero con un poco de paciencia y curiosidad, estoy seguro de que lo entenderás completamente. Así que, sin más preámbulos, ¡comencemos!
¿Qué son los números irracionales?
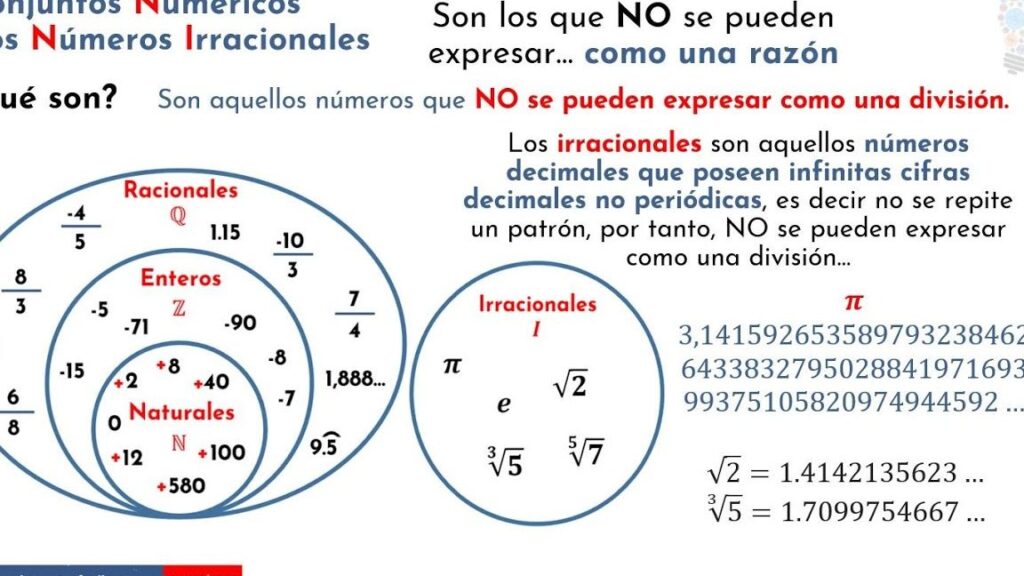
Los números irracionales son aquellos números que no pueden ser expresados como una fracción de dos enteros. En otras palabras, no se pueden escribir como a/b, donde a y b son enteros y b no es cero. Los números irracionales tienen una expansión decimal infinita y no periódica, lo que significa que no tienen un patrón repetitivo.
Ejemplos de números irracionales
Algunos de los ejemplos más conocidos de números irracionales son:
- √2 (la raíz cuadrada de 2)
- π (pi)
- e (la base del logaritmo natural)
Estos números tienen propiedades únicas y aparecen en diversas ramas de las matemáticas y la ciencia.
La historia de los números irracionales
La historia de los números irracionales se remonta a la antigua Grecia. Los matemáticos griegos, como Pitágoras, inicialmente creían que todos los números podían ser expresados como fracciones. Sin embargo, el descubrimiento de la raíz cuadrada de 2, que no podía ser expresada como una fracción, desafió esta creencia y llevó a la aceptación de los números irracionales.
El descubrimiento de √2
Se dice que uno de los seguidores de Pitágoras, Hipaso de Metaponto, fue quien descubrió que la raíz cuadrada de 2 no podía ser expresada como una fracción. Este descubrimiento fue tan impactante que, según la leyenda, Hipaso fue castigado por los pitagóricos, quienes preferían mantener este conocimiento en secreto.
Propiedades de los números irracionales
Los números irracionales tienen varias propiedades interesantes:
- No pueden ser expresados como fracciones.
- Tienen una expansión decimal infinita y no periódica.
- Son números reales, lo que significa que pueden ser representados en la recta numérica.
- La suma o el producto de un número racional y un número irracional es siempre irracional.
Cómo distinguir entre números racionales e irracionales
Para distinguir entre números racionales e irracionales, puedes seguir estos pasos:
- Intenta expresar el número en forma de fracción. Si puedes hacerlo, es un número racional.
- Examina la expansión decimal del número. Si tiene una expansión infinita y no periódica, es irracional.
- Utiliza la teoría de números y propiedades matemáticas para identificar si el número es irracional.
Importancia de los números irracionales en la matemática
Los números irracionales juegan un papel crucial en la matemática. Aparecen en diversas áreas, como el cálculo, la geometría y la teoría de números. Por ejemplo, π es fundamental en la geometría y aparece en las fórmulas para el área y el perímetro de un círculo. La constante e es esencial en el cálculo y aparece en diversas fórmulas relacionadas con el crecimiento exponencial y los logaritmos.
Aplicaciones de los números irracionales en la vida real
Los números irracionales no solo son importantes en la teoría matemática, sino que también tienen aplicaciones prácticas en la vida real. Algunos ejemplos incluyen:
- Ingeniería: Los números irracionales se utilizan en el diseño de estructuras y en la ingeniería civil.
- Física: Aparecen en diversas fórmulas físicas, como la constante de Planck y la ecuación de Schrödinger.
- Economía: La constante e se utiliza en modelos de crecimiento exponencial y en cálculos financieros.
Desafíos en la comprensión de los números irracionales
Uno de los mayores desafíos en la comprensión de los números irracionales es su naturaleza infinita y no periódica. Esto puede ser difícil de visualizar y comprender. Sin embargo, con la práctica y el estudio, puedes llegar a comprenderlos mejor.
Recursos adicionales para entender los números irracionales
Si estás interesado en profundizar en el estudio de los números irracionales, aquí tienes algunos recursos adicionales:
Conclusión
Espero que este artículo te haya ayudado a entender mejor los números irracionales. Aunque pueden parecer complicados al principio, con el tiempo y la práctica, verás que son una parte fundamental y fascinante de las matemáticas. Recuerda que la clave para entender los números irracionales es la paciencia y la curiosidad. ¡Sigue explorando y aprendiendo!
