Todo lo que Necesitas Saber
¡Hola a todos! Soy Leandro, y hoy vamos a hablar de uno de mis temas favoritos en matemáticas: el producto escalar. Con años de experiencia en la enseñanza y aplicación de conceptos matemáticos, estoy aquí para desglosar este tema de una manera que sea fácil de entender y, sobre todo, útil. Así que, ¡vamos allá!
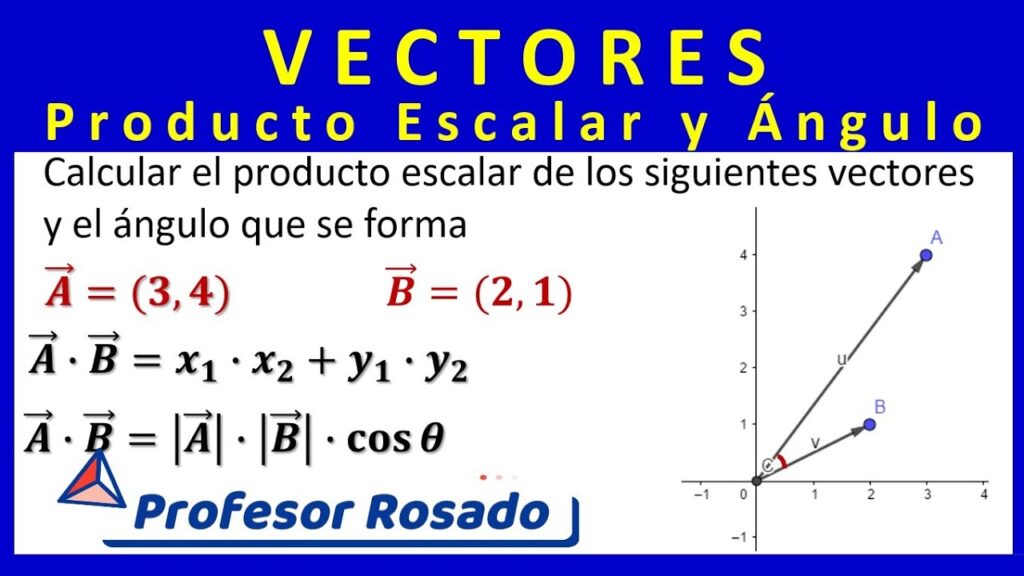
¿Qué es el Producto Escalar?
El producto escalar, también conocido como multiplicación escalar o producto punto, es una operación matemática que se realiza entre dos vectores. La idea es sencilla: tomas dos vectores y los multiplicas para obtener un único número, que es el producto escalar.
En términos matemáticos, si tienes dos vectores a y b, el producto escalar se denota como a · b y se calcula como:
a · b = a1b1 + a2b2 + … + anbn
¿Qué Significa el Resultado del Producto Escalar?
El resultado del producto escalar es un número real que nos da información sobre la relación entre los dos vectores. Si el producto escalar es cero, significa que los vectores son perpendiculares entre sí. Si es positivo, indica que los vectores tienen una dirección similar, y si es negativo, apunta a que tienen direcciones opuestas.
Propiedades del Producto Escalar
Como toda operación matemática, el producto escalar tiene una serie de propiedades que lo hacen particularmente interesante y útil. Aquí te presento algunas de las más importantes:
- Conmutatividad: a · b = b · a
- Distributividad: a · (b + c) = a · b + a · c
- Asociatividad con el Escalar: k(a · b) = (ka) · b = a · (kb) donde k es un número real.
- Producto Escalar de un Vector Consigo Mismo: a · a = |a|², donde |a| es la magnitud del vector a.
Aplicaciones del Producto Escalar
El producto escalar no es solo un concepto teórico; tiene múltiples aplicaciones prácticas en diversos campos. A continuación, te presento algunas de las más comunes:
En Física
En el campo de la física, el producto escalar se utiliza para calcular el trabajo realizado por una fuerza. La fórmula es:
Trabajo = Fuerza · Desplazamiento
Esto nos permite entender cuánto esfuerzo se ha puesto en mover un objeto a lo largo de una distancia determinada.
En Computación Gráfica
En computación gráfica, el producto escalar se utiliza para determinar el ángulo entre dos vectores, lo que es crucial para la iluminación y sombreado en gráficos 3D. Esto ayuda a crear imágenes más realistas.
En Matemáticas Puras
Dentro del campo de las matemáticas, el producto escalar es fundamental en álgebra lineal. Se utiliza para definir y trabajar con espacios vectoriales y subespacios, así como en la teoría de matrices.
Comparación con Otros Productos entre Vectores
Es natural que te preguntes cómo se compara el producto escalar con otros tipos de productos entre vectores, como el producto vectorial. Vamos a echar un vistazo rápido a las diferencias clave:
Producto Escalar vs Producto Vectorial
Mientras que el producto escalar da como resultado un número real, el producto vectorial produce otro vector. El producto vectorial se utiliza principalmente en tres dimensiones y es útil en física y geometría.
La fórmula del producto vectorial entre dos vectores a y b es:
a × b = (a2b3 – a3b2, a3b1 – a1b3, a1b2 – a2b1)
En resumen, el producto escalar es más sencillo y se utiliza para fines diferentes en comparación con el producto vectorial.
Cómo Calcular el Producto Escalar
Para que te quede aún más claro, vamos a ver paso a paso cómo calcular el producto escalar entre dos vectores.
Paso 1: Identificar los Componentes de los Vectores
Supongamos que tenemos dos vectores en el espacio tridimensional:
a = (a1, a2, a3) y b = (b1, b2, b3)
Paso 2: Multiplicar los Componentes Correspondientes
Multiplicamos los componentes correspondientes de cada vector:
a1b1, a2b2, a3b3
Paso 3: Sumar los Productos
Finalmente, sumamos los productos obtenidos:
a · b = a1b1 + a2b2 + a3b3
¡Y listo! Ya tenemos el producto escalar.
Ejemplo Práctico
Vamos a ver un ejemplo práctico para que todo quede aún más claro. Supongamos que tenemos los siguientes vectores:
a = (1, 2, 3) y b = (4, 5, 6)
El producto escalar sería:
a · b = 1*4 + 2*5 + 3*6 = 4 + 10 + 18 = 32
Así de fácil es calcular el producto escalar.
Herramientas y Recursos para Aprender Más
Si este artículo ha despertado tu interés y quieres profundizar más en el tema, te recomiendo algunos recursos adicionales. Hay muchos cursos en línea, libros y tutoriales que pueden ayudarte a entender mejor el producto escalar y otros conceptos relacionados.
Conclusión
El producto escalar es una herramienta matemática poderosa y versátil con aplicaciones prácticas en muchos campos. Desde la física hasta la computación gráfica, pasando por las matemáticas puras, entender este concepto puede abrirte muchas puertas. Espero que este artículo te haya sido útil y te haya aclarado cualquier duda que pudieras tener.
