Análisis y Explicaciones
Introducción a la Posición Relativa de Tres Planos
¡Hola! Soy Leandro y hoy vamos a sumergirnos en el fascinante mundo de la geometría tridimensional. Si alguna vez te has preguntado cómo interactúan tres planos en el espacio, estás en el lugar correcto. A menudo, este tema puede parecer un poco abstracto, pero te aseguro que con un poco de paciencia y curiosidad, todo se vuelve claro como el agua. Vamos a explorar la posición relativa de tres planos, sus posibles intersecciones y cómo determinarlas.
Conceptos Básicos para Entender la Posición Relativa de Tres Planos
Antes de profundizar en la posición relativa de tres planos, es crucial entender algunos conceptos básicos. Un plano en el espacio tridimensional se define por una ecuación de la forma Ax + By + Cz + D = 0. Aquí, A, B, C y D son constantes que determinan la orientación y la posición del plano.
Cuando hablamos de la posición relativa de tres planos, estamos interesados en cómo se intersectan o no se intersectan entre sí. Las posiciones relativas pueden clasificarse en varias categorías, que exploraremos a continuación.
Categorías de la Posición Relativa de Tres Planos
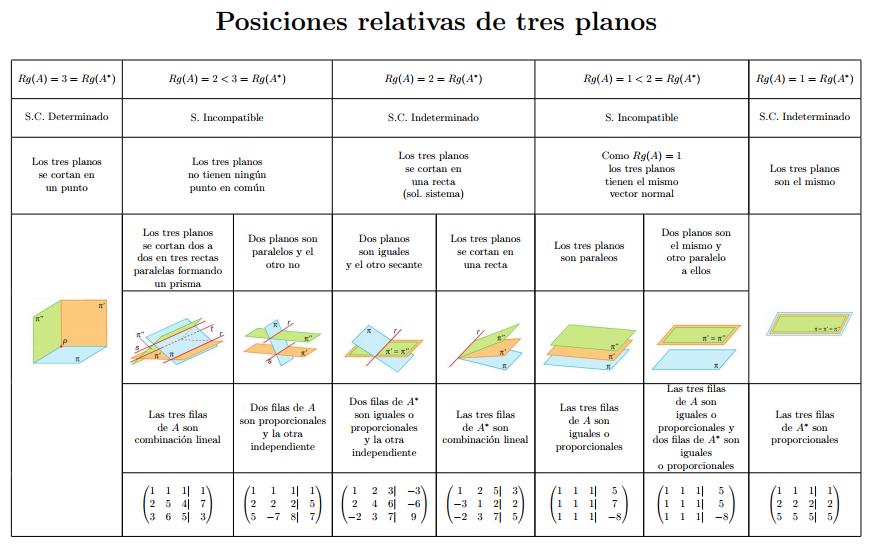
Existen varias formas en las que tres planos pueden interactuar en el espacio tridimensional. Aquí te presento las principales categorías:
1. Tres Planos Paralelos
En este caso, los tres planos no se intersectan en ningún punto. Cada uno de ellos es paralelo a los otros dos. Para que esto ocurra, las normales de los planos deben ser proporcionales. Este caso es bastante sencillo de identificar y entender.
2. Dos Planos Paralelos y el Tercero No
Aquí, dos de los planos son paralelos entre sí y el tercero intersecta a ambos. Este es un caso intermedio y es bastante común en problemas geométricos.
3. Tres Planos que se Intersectan en una Línea Común
En esta configuración, los tres planos se intersectan en una línea común. Esto ocurre cuando las ecuaciones de los planos tienen soluciones en común que forman una línea.
4. Tres Planos que se Intersectan en un Punto Común
Este es quizás el caso más interesante. Los tres planos se intersectan en un único punto. Esto ocurre cuando las tres ecuaciones tienen una solución única.
5. Tres Planos que se Intersectan en un Punto y una Línea
En este caso, dos de los planos se intersectan a lo largo de una línea y el tercer plano intersecta esa línea en un único punto, pero no es paralelo a ninguno de los dos primeros planos.
6. Tres Planos que se Intersectan en Tres Líneas Concurrentes
Finalmente, los tres planos pueden intersectarse en tres líneas que se encuentran en un único punto. Este es un caso más complejo y menos común, pero es fascinante de analizar.
Métodos para Determinar la Posición Relativa de Tres Planos
Ahora que conocemos las diferentes categorías de la posición relativa de tres planos, es importante entender cómo determinar en qué categoría se encuentra un conjunto dado de planos. Aquí te presento algunos métodos y herramientas:
1. Método Algebraico
El método algebraico consiste en resolver el sistema de ecuaciones lineales formado por las ecuaciones de los tres planos. Dependiendo de las soluciones que obtengas (una solución única, infinitas soluciones o ninguna solución), podrás determinar la posición relativa de los planos.
2. Análisis Vectorial
El análisis vectorial es otra herramienta poderosa. Puedes utilizar vectores normales a los planos para determinar si son paralelos o si se intersectan. Las relaciones entre los vectores normales te darán pistas sobre la posición relativa de los planos.
3. Uso de Software de Geometría
En la era digital, tenemos la ventaja de utilizar software de geometría como GeoGebra o MATLAB para visualizar y analizar la posición relativa de tres planos. Estas herramientas pueden simplificar mucho el proceso y proporcionar representaciones visuales claras.
Aplicaciones Prácticas de la Posición Relativa de Tres Planos
Entender la posición relativa de tres planos no es solo un ejercicio académico; tiene aplicaciones prácticas en diversas áreas. Aquí te dejo algunos ejemplos:
1. Arquitectura y Construcción
En arquitectura y construcción, es crucial entender cómo se intersectan diferentes planos para diseñar estructuras estables y funcionales. Los ingenieros utilizan estos conceptos para planificar la disposición de paredes, techos y otros elementos estructurales.
2. Gráficos por Computadora
En gráficos por computadora, la intersección de planos es fundamental para renderizar escenas tridimensionales. Los motores gráficos utilizan algoritmos basados en la posición relativa de planos para determinar cómo se proyectan y se visualizan los objetos en la pantalla.
3. Física y Matemáticas
En física y matemáticas, la intersección de planos aparece en diversos problemas, desde la mecánica cuántica hasta la teoría de la relatividad. Entender cómo interactúan los planos es esencial para resolver estos problemas y desarrollar nuevas teorías.
Competencia y Recursos Adicionales
Existen varios recursos en línea que abordan el tema de la posición relativa de tres planos. Aquí te dejo algunos enlaces útiles para profundizar en el tema:
En cuanto a la competencia, varios sitios web y blogs también abordan este tema, pero muchos de ellos se centran en explicaciones teóricas sin profundizar en aplicaciones prácticas. Por eso, creo que este artículo ofrece un enfoque más completo y práctico.
Conclusión: La Importancia de Entender la Posición Relativa de Tres Planos
En resumen, la posición relativa de tres planos es un tema fascinante y de gran importancia en diversas áreas. Desde la arquitectura hasta la física, entender cómo interactúan los planos en el espacio tridimensional nos permite resolver problemas complejos y desarrollar nuevas aplicaciones.
Espero que este artículo te haya sido útil y que ahora tengas una mejor comprensión de este tema.
