Introducción a la Posición Relativa de Dos Planos
¡Hola a todos! Soy Leandro, y hoy vamos a sumergirnos en el fascinante mundo de la geometría para hablar sobre la posición relativa de dos planos. Este tema, aunque pueda parecer un poco abstracto al principio, tiene muchas aplicaciones prácticas y es fundamental en áreas como la arquitectura, la ingeniería y las matemáticas. Vamos a desglosarlo de manera sencilla y comprensible para que todos podamos entenderlo.
¿Qué es la Posición Relativa de Dos Planos?
Antes de adentrarnos en las diferentes posiciones que pueden tener dos planos, es importante definir qué entendemos por «posición relativa». En términos sencillos, la posición relativa de dos planos se refiere a cómo se relacionan o interactúan entre sí en el espacio tridimensional.
Existen varias posibles relaciones entre dos planos, y estas pueden clasificarse principalmente en tres categorías:
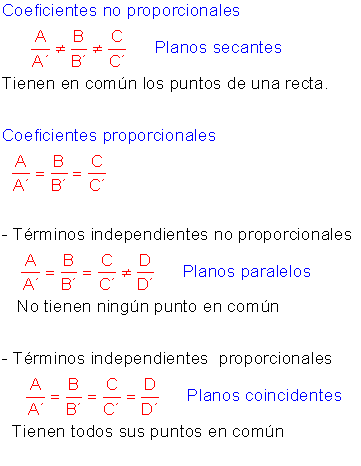
- Planos Paralelos: Los planos nunca se cruzan, no tienen puntos en común.
- Planos Secantes: Los planos se cruzan en una línea.
- Planos Coincidentes: Los planos son el mismo, tienen todos sus puntos en común.
Planos Paralelos
Empezamos con los planos paralelos. Estos son aquellos que, aunque se prolonguen indefinidamente, nunca se van a encontrar. Puedes imaginar dos hojas de papel colocadas una encima de la otra sin tocarse. Eso es esencialmente lo que son dos planos paralelos.
Para determinar si dos planos son paralelos, podemos examinar sus ecuaciones. Si las normales (vectores perpendiculares) de los planos son proporcionales, entonces los planos son paralelos. Por ejemplo, si tenemos dos planos con ecuaciones:
Plano 1: Ax + By + Cz + D1 = 0
Plano 2: k(Ax + By + Cz) + D2 = 0
Si el vector normal del Plano 1 es (A, B, C) y el vector normal del Plano 2 es k(A, B, C), entonces los planos son paralelos.
Planos Secantes
Ahora hablemos de los planos secantes. Estos son los planos que se cruzan en una línea. Imagina una hoja de papel que corta otra hoja en un ángulo. La línea de intersección es donde estos dos planos se cruzan.
Para determinar si dos planos son secantes, simplemente resolvemos sus ecuaciones simultáneamente. Si encontramos una línea de intersección, entonces los planos son secantes. Por ejemplo, consideremos los siguientes planos:
Plano 1: Ax + By + Cz + D1 = 0
Plano 2: Ex + Fy + Gz + D2 = 0
Al resolver este sistema de ecuaciones, si encontramos una línea de intersección, entonces los planos son secantes.
Planos Coincidentes
Finalmente, tenemos los planos coincidentes. Estos son los planos que son esencialmente el mismo plano, es decir, tienen todos sus puntos en común. Puedes pensar en esto como dos hojas de papel que se superponen perfectamente.
Para determinar si dos planos son coincidentes, sus ecuaciones deben ser múltiplos exactos entre sí. Por ejemplo, si tenemos dos planos con ecuaciones:
Plano 1: Ax + By + Cz + D1 = 0
Plano 2: k(Ax + By + Cz + D1) = 0
Si podemos encontrar un valor de k tal que las ecuaciones sean idénticas, entonces los planos son coincidentes.
Aplicaciones Prácticas de la Posición Relativa de Dos Planos
Ahora que hemos cubierto las bases teóricas, es momento de ver algunas aplicaciones prácticas de la posición relativa de dos planos. Este conocimiento es esencial en muchas disciplinas. Aquí hay algunos ejemplos:
Arquitectura e Ingeniería
En arquitectura, entender la posición relativa de dos planos es crucial para diseñar edificios y estructuras. Por ejemplo, los arquitectos deben asegurarse de que los pisos de un edificio sean paralelos para garantizar la estabilidad estructural.
Diseño Gráfico y Modelado 3D
En el diseño gráfico y el modelado 3D, los diseñadores a menudo trabajan con múltiples planos para crear objetos tridimensionales. Saber cómo interactúan estos planos entre sí es fundamental para crear modelos precisos y realistas.
Matemáticas y Física
En matemáticas y física, la comprensión de la posición relativa de los planos es esencial para resolver problemas complejos. Por ejemplo, en la física cuántica, los planos pueden representar diferentes estados de energía, y su interacción puede tener implicaciones significativas.
Recursos Adicionales
Para aquellos que quieran profundizar en este tema, aquí hay algunos recursos adicionales que pueden resultar útiles:
Conclusión
Espero que este artículo haya arrojado algo de luz sobre el tema de la posición relativa de dos planos. Como hemos visto, entender cómo se relacionan los planos entre sí es fundamental en muchas disciplinas. Ya sea que estés diseñando un edificio, creando un modelo 3D o resolviendo un problema matemático complejo, este conocimiento te será invaluable.
