Guía Completa
Introducción a la Ecuación Recta en el Espacio
Hola, soy Leandro, y hoy vamos a sumergirnos en el fascinante mundo de la ecuación recta en el espacio. Ya sé, ya sé, puede sonar un poco intimidante al principio, pero te aseguro que, con un poco de paciencia y mucha curiosidad, entenderás todo sobre este tema. La ecuación recta en el espacio es una herramienta fundamental en matemáticas y física, y su comprensión puede abrirte la puerta a un sinfín de aplicaciones prácticas.
¿Qué es la Ecuación Recta en el Espacio?
Para empezar, definamos qué es una ecuación recta en el espacio. Básicamente, es una representación matemática que describe una línea recta en un espacio tridimensional. A diferencia de la ecuación de la recta en el plano, que se limita a dos dimensiones (x e y), la ecuación recta en el espacio incluye una tercera dimensión, z. Esto nos permite modelar y analizar situaciones en un entorno 3D, lo que es increíblemente útil en campos como la ingeniería, la arquitectura y la física.
Formas de Representar una Recta en el Espacio
Hay varias maneras de representar una recta en el espacio. Las más comunes son la forma vectorial y la forma paramétrica. Ambas tienen sus propias ventajas y aplicaciones, así que echemos un vistazo más de cerca a cada una de ellas.
Forma Vectorial
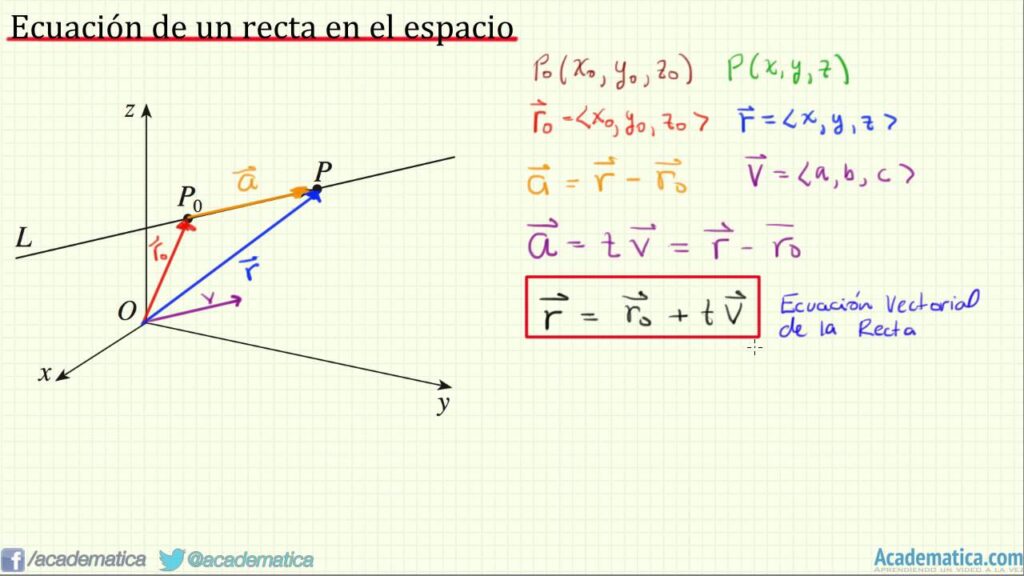
La forma vectorial de una recta en el espacio se expresa como:
mathbf{r} = mathbf{r}_0 + tmathbf{d}
Aquí, (mathbf{r}) es el vector de posición de un punto cualquiera en la recta, (mathbf{r}_0) es el vector de posición de un punto específico en la recta, (mathbf{d}) es el vector director que indica la dirección de la recta, y (t) es un parámetro que puede tomar cualquier valor real.
Forma Paramétrica
La forma paramétrica de una recta en el espacio se representa mediante tres ecuaciones, una para cada coordenada:
x = x_0 + t d_x
y = y_0 + t d_y
z = z_0 + t d_z
Aquí, ((x_0, y_0, z_0)) son las coordenadas de un punto en la recta, ((d_x, d_y, d_z)) son las componentes del vector director, y (t) es el parámetro que varía.
Aplicaciones de la Ecuación Recta en el Espacio
La ecuación recta en el espacio tiene numerosas aplicaciones prácticas. Aquí te dejo algunas de las más destacadas:
Ingeniería y Arquitectura
En estos campos, la ecuación recta en el espacio se utiliza para diseñar estructuras y sistemas que deben funcionar en un entorno tridimensional. Por ejemplo, los ingenieros civiles la utilizan para calcular la resistencia de puentes y edificios, mientras que los arquitectos la usan para crear planos y modelos 3D.
Física
En física, la ecuación recta en el espacio es fundamental para describir el movimiento de partículas y objetos en el espacio. Desde la trayectoria de un proyectil hasta la órbita de un satélite, esta herramienta matemática es esencial para entender el comportamiento de los cuerpos en movimiento.
Gráficos por Computadora
En el mundo de los gráficos por computadora, la ecuación recta en el espacio se utiliza para generar y manipular imágenes 3D. Desde la creación de videojuegos hasta la animación por computadora, esta ecuación es fundamental para renderizar escenas tridimensionales de manera precisa y realista.
Comparación con Otras Ecuaciones
Es común preguntarse cómo se compara la ecuación recta en el espacio con otras ecuaciones similares, como la ecuación de la recta en el plano. Vamos a explorar algunas de las diferencias clave.
Ecuación Recta en el Plano vs. Ecuación Recta en el Espacio
La principal diferencia entre estas dos ecuaciones es la dimensión en la que operan. La ecuación recta en el plano se limita a dos dimensiones, mientras que la ecuación recta en el espacio incluye una tercera dimensión. Esto hace que la ecuación recta en el espacio sea más compleja, pero también más versátil y aplicable a una mayor variedad de situaciones.
Ecuación de la Recta en Coordenadas Cartesianas
Otra comparación interesante es con la ecuación de la recta en coordenadas cartesianas, que se expresa como (y = mx + b). Aunque esta forma es muy útil para representar rectas en el plano, no es adecuada para describir rectas en el espacio tridimensional. La ecuación recta en el espacio, en sus formas vectorial y paramétrica, es mucho más adecuada para este propósito.
Ejemplos Prácticos y Ejercicios
Para comprender mejor cómo funciona la ecuación recta en el espacio, vamos a ver algunos ejemplos prácticos y ejercicios que puedes intentar por tu cuenta.
Ejemplo 1: Forma Vectorial
Supongamos que tenemos un punto (P(1, 2, 3)) y un vector director (mathbf{d} = (4, 5, 6)). La ecuación vectorial de la recta que pasa por (P) y tiene la dirección de (mathbf{d}) es:
mathbf{r} = (1, 2, 3) + t(4, 5, 6)
Aquí, (t) puede tomar cualquier valor real, lo que nos da todos los puntos en la recta.
Ejemplo 2: Forma Paramétrica
Usando el mismo punto y vector director del ejemplo anterior, las ecuaciones paramétricas serían:
x = 1 + 4t
y = 2 + 5t
z = 3 + 6t
Nuevamente, (t) puede variar, proporcionando todos los puntos en la recta.
Ejercicio
Ahora es tu turno. Supón que tienes un punto (Q(2, -1, 5)) y un vector director (mathbf{d} = (-3, 4, 1)). Escribe la ecuación vectorial y las ecuaciones paramétricas de la recta que pasa por (Q) y tiene la dirección de (mathbf{d}).
Recursos Adicionales
Para aquellos que quieran profundizar más en el tema, aquí hay algunos recursos adicionales que pueden ser de gran ayuda:
Conclusión
En resumen, la ecuación recta en el espacio es una herramienta matemática poderosa y versátil que tiene aplicaciones en numerosos campos. Desde la ingeniería hasta la física y los gráficos por computadora, su comprensión es esencial para cualquiera que trabaje en un entorno tridimensional. Espero que esta guía te haya sido útil y que ahora te sientas más cómodo trabajando con la ecuación recta en el espacio. ¡Hasta la próxima!
