Introducción a las Potencias

¡Hola! Soy Leandro, y hoy vamos a sumergirnos en el fascinante mundo de las potencias. Este concepto matemático es fundamental en muchas áreas, desde la física hasta la economía. A lo largo de este artículo, te explicaré de manera clara y sencilla qué son las potencias, cómo se utilizan y por qué son tan importantes.

¿Qué Son las Potencias?

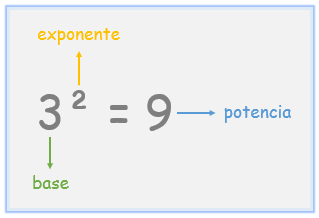
Las potencias son una forma abreviada de expresar la multiplicación repetida de un número por sí mismo. En términos simples, si tienes un número a y lo multiplicas por sí mismo n veces, se dice que a está elevado a la n-ésima potencia. Se representa como aⁿ, donde a es la base y n es el exponente.

Ejemplo de Potencia

Imagina que tienes el número 2 y lo multiplicas por sí mismo 3 veces. Esto se escribiría como 2³, lo que es igual a 2 * 2 * 2 = 8.

Notación de las Potencias

La notación de potencias es una herramienta poderosa que simplifica la escritura y el cálculo de multiplicaciones repetidas. En lugar de escribir 2 * 2 * 2 * 2 * 2, puedes escribir simplemente 2⁵. Esto no solo ahorra espacio, sino que también facilita el análisis y la manipulación de expresiones matemáticas complejas.

Importancia de las Potencias en Matemáticas y Ciencia

Las potencias son cruciales en diversas áreas del conocimiento. En matemáticas, son fundamentales en el estudio de funciones exponenciales y logarítmicas. En física, se utilizan para describir fenómenos como el crecimiento exponencial y la desintegración radiactiva. Además, las potencias son esenciales en la economía para calcular el interés compuesto y en la informática para trabajar con grandes cantidades de datos.

Funciones Exponenciales

Las funciones exponenciales son aquellas en las que una constante se eleva a una variable. Estas funciones son esenciales en el estudio del crecimiento y la desintegración en diversos contextos, como la biología y la economía. Por ejemplo, el crecimiento poblacional puede modelarse mediante una función exponencial.

Interés Compuesto

En economía, el interés compuesto se calcula utilizando potencias. Si inviertes una cantidad de dinero a una tasa de interés específica, la cantidad total de dinero crece de manera exponencial con el tiempo. La fórmula para calcular el interés compuesto es P(1 + r/n)^nt, donde P es el principal, r es la tasa de interés, n es el número de veces que se compone el interés en un año y t es el tiempo en años.

Propiedades de las Potencias

Las potencias tienen varias propiedades que facilitan el cálculo y la manipulación de expresiones matemáticas. A continuación, se presentan algunas de las propiedades más importantes:

Producto de Potencias con la Misma Base

Si tienes dos potencias con la misma base, puedes multiplicarlas sumando sus exponentes. Por ejemplo, a^m * aⁿ = a^m+n.

Cociente de Potencias con la Misma Base

Si tienes dos potencias con la misma base, puedes dividirlas restando sus exponentes. Por ejemplo, a^m / aⁿ = a^m-n.

Potencia de una Potencia

Si tienes una potencia de una potencia, puedes multiplicar los exponentes. Por ejemplo, (a^m)ⁿ = a^m*n.

Potencia de un Producto

Si tienes un producto elevado a una potencia, puedes elevar cada factor a esa potencia. Por ejemplo, (ab)ⁿ = aⁿ * bⁿ.

Aplicaciones de las Potencias en la Vida Cotidiana

Las potencias no son solo un concepto abstracto en las matemáticas; tienen aplicaciones prácticas en la vida diaria. A continuación, se presentan algunas formas en que las potencias se utilizan en situaciones cotidianas:

Cálculo de Intereses

Como mencioné anteriormente, las potencias se utilizan para calcular el interés compuesto. Esto es esencial para la planificación financiera y la inversión.

Escalas de Medición

Las potencias se utilizan en las escalas de medición, como la escala de Richter para medir la magnitud de los terremotos y la escala de decibelios para medir la intensidad del sonido.

Computación

En la informática, las potencias son esenciales para trabajar con grandes cantidades de datos. Los algoritmos de búsqueda y clasificación, así como la criptografía, se basan en cálculos exponenciales.