Todo lo que Necesitas Saber
Introducción a los Logaritmos
¡Hola! Soy Leandro, un apasionado de las matemáticas, y hoy quiero compartir contigo todo lo que sé sobre los logaritmos. Este tema puede sonar un poco intimidante al principio, pero te aseguro que, con un poco de paciencia y curiosidad, verás que es fascinante y muy útil. Así que, sin más preámbulos, vamos a sumergirnos en el mundo de los logaritmos.
¿Qué son los Logaritmos?
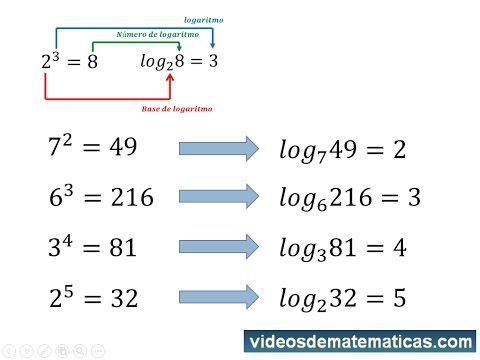
Los logaritmos son una herramienta matemática que nos permite resolver ecuaciones exponenciales. En pocas palabras, un logaritmo nos dice a qué exponente debemos elevar una base para obtener un cierto número. Por ejemplo, el logaritmo en base 10 de 100 es 2, porque 10 elevado a la 2 es 100. La notación matemática de esto es log10(100) = 2.
En términos más formales, si tenemos una base b y un número y, el logaritmo de y en base b es un número x tal que b elevado a la x es igual a y. Esto se escribe como logb(y) = x.
Historia de los Logaritmos
La historia de los logaritmos es tan interesante como su definición. Fueron introducidos por John Napier en el siglo XVII como una forma de simplificar los cálculos matemáticos. Antes de que existieran las calculadoras y computadoras, los logaritmos eran una herramienta esencial para científicos y matemáticos. Napier publicó su obra «Mirifici Logarithmorum Canonis Descriptio» en 1614, donde presentó sus logaritmos y tablas para su uso.
Otro nombre importante en la historia de los logaritmos es Henry Briggs, quien colaboró con Napier y desarrolló los logaritmos en base 10, conocidos también como logaritmos comunes o decimales. Estos logaritmos comunes se volvieron extremadamente populares y fueron ampliamente utilizados hasta la llegada de las calculadoras electrónicas.
Propiedades de los Logaritmos
Los logaritmos tienen varias propiedades importantes que los hacen útiles para simplificar cálculos complejos. Aquí te dejo algunas de las más relevantes:
Propiedad del Producto
La propiedad del producto dice que el logaritmo de un producto es igual a la suma de los logaritmos de los factores. Matemáticamente, esto se expresa como:
logb(xy) = logb(x) + logb(y)
Propiedad del Cociente
La propiedad del cociente establece que el logaritmo de un cociente es igual a la diferencia de los logaritmos del numerador y el denominador:
logb(x/y) = logb(x) – logb(y)
Propiedad de la Potencia
Esta propiedad indica que el logaritmo de una potencia es igual al exponente multiplicado por el logaritmo de la base:
logb(xy) = y * logb(x)
Cambio de Base
La fórmula de cambio de base permite convertir un logaritmo de una base a otra. La fórmula es la siguiente:
logb(x) = logk(x) / logk(b)
Esta propiedad es especialmente útil cuando necesitas calcular logaritmos en una base para la cual no tienes una calculadora.
Aplicaciones de los Logaritmos
Los logaritmos tienen una amplia gama de aplicaciones en diferentes campos. Aquí te presento algunas de las más importantes:
Matemáticas y Estadística
En matemáticas, los logaritmos se utilizan en la resolución de ecuaciones exponenciales, en el cálculo diferencial e integral, y en la teoría de números. En estadística, los logaritmos se usan para transformar datos, especialmente cuando se trabaja con datos que abarcan varios órdenes de magnitud.
Ingeniería y Física
En ingeniería y física, los logaritmos son esenciales para trabajar con fenómenos que varían exponencialmente, como el crecimiento poblacional, la desintegración radiactiva y la atenuación del sonido. También se utilizan en la escala de Richter para medir la magnitud de los terremotos y en la escala de decibelios para medir la intensidad del sonido.
Informática
En informática, los logaritmos juegan un papel crucial en algoritmos de búsqueda y clasificación. Por ejemplo, el algoritmo de búsqueda binaria tiene una complejidad de tiempo de O(log n), lo que significa que su eficiencia mejora logarítmicamente con el tamaño de los datos.
Economía y Finanzas
En economía y finanzas, los logaritmos se utilizan para modelar el crecimiento compuesto y las tasas de interés. También se usan en la evaluación de riesgos y en la teoría de carteras.
Calculadoras y Herramientas para Logaritmos
Hoy en día, calcular logaritmos es más fácil que nunca gracias a las calculadoras científicas y las herramientas en línea. Algunas de las mejores opciones incluyen:
- Desmos: Una potente calculadora gráfica en línea que soporta logaritmos.
- Symbolab: Una calculadora avanzada que puede resolver ecuaciones logarítmicas paso a paso.
- Wolfram Alpha: Una herramienta de computación de conocimiento que puede calcular logaritmos y mucho más.
Logaritmos en la Educación
Los logaritmos son una parte fundamental del currículo de matemáticas en la educación secundaria y universitaria. Aprender a trabajar con logaritmos no solo es esencial para avanzar en matemáticas, sino que también desarrolla habilidades de pensamiento crítico y resolución de problemas que son valiosas en muchas áreas del conocimiento.
Para aquellos que buscan recursos adicionales, hay muchos sitios web y plataformas educativas que ofrecen lecciones y ejercicios sobre logaritmos. Algunos de los más recomendados son:
- Khan Academy: Ofrece lecciones y prácticas interactivas sobre logaritmos.
- Coursera: Cursos en línea que incluyen temas de matemáticas avanzadas, incluyendo logaritmos.
- edX: Cursos en línea de universidades reconocidas que cubren logaritmos y otras áreas de matemáticas.
Comparación con Otras Herramientas Matemáticas
Los logaritmos no son la única herramienta matemática para tratar con escalas y crecimientos exponenciales. Aquí hay una breve comparación con otras herramientas similares:
Exponentes
Mientras que los logaritmos nos dicen a qué exponente elevar una base para obtener un determinado número, los exponentes nos dicen el resultado de elevar una base a una potencia. Ambos conceptos son inversos el uno del otro.
Funciones Exponenciales
Las funciones exponenciales describen el crecimiento o la disminución de una cantidad a un ritmo que es proporcional a su valor actual. Los logaritmos son útiles para describir el tiempo requerido para que una cantidad crezca a un cierto valor en una función exponencial.
Series y Sucesiones
Las series y sucesiones son otras herramientas matemáticas que se utilizan para describir crecimientos y patrones. Aunque no están directamente relacionadas con los logaritmos, pueden ser utilizadas en combinación con ellos para resolver problemas complejos.
Conclusión
Espero que este artículo te haya ayudado a entender mejor qué son los logaritmos, cómo se utilizan y por qué son tan importantes. Desde sus humildes comienzos en el siglo XVII hasta su uso en la tecnología moderna, los logaritmos han demostrado ser una herramienta matemática increíblemente poderosa. Así que la próxima vez que te encuentres con un problema que involucre logaritmos, recuerda que tienes una herramienta poderosa a tu disposición para simplificar y resolverlo.
