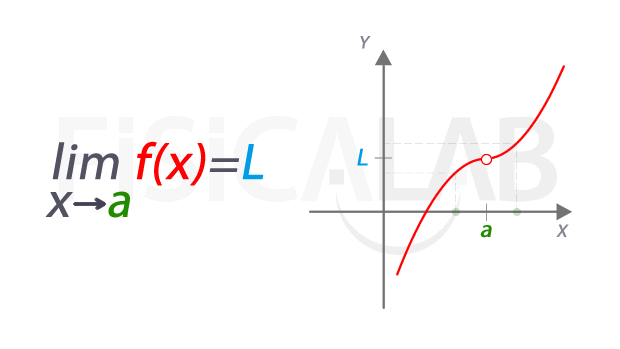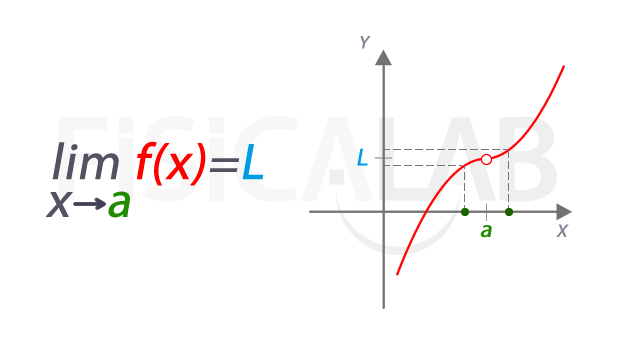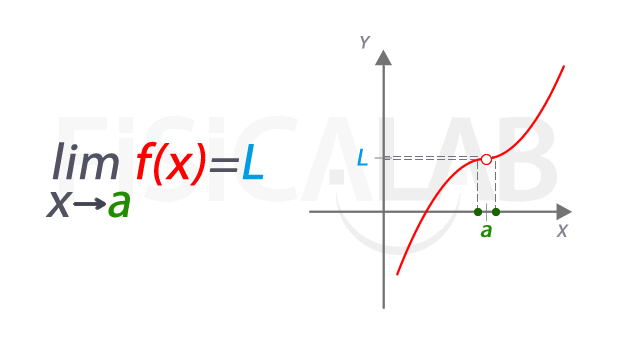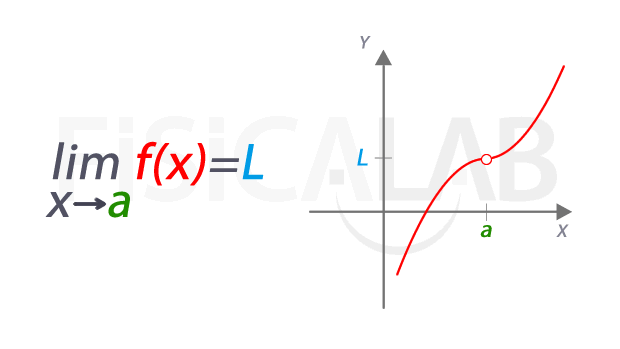
Una Explicación Experta por Leandro
Introducción al Concepto de Límite en un Punto
¡Hola a todos! Soy Leandro, y hoy quiero hablarles de un concepto fundamental en el análisis matemático: el límite en un punto. No sé ustedes, pero para mí, entender los límites fue un punto de inflexión en mi carrera académica. Así que, si estás aquí para conocer más sobre los límites, estás en el lugar correcto.
¿Qué es un Límite en un Punto?
Vamos al grano. Un límite en un punto es una herramienta matemática que nos permite describir el comportamiento de una función a medida que se aproxima a un valor específico. En otras palabras, nos interesa saber qué valor toma una función cuando su variable independiente se acerca a un punto determinado. Es una idea poderosa que subyace en gran parte del cálculo y análisis matemático.
Definición Formal de Límite en un Punto
Para ser más precisos, la definición formal es la siguiente: Si f(x) es una función y a es un punto en su dominio, decimos que el límite de f(x) cuando x tiende a a es L, y escribimos:
limx→a f(x) = L
Si, para cada número ε > 0, existe un número δ > 0 tal que cuando 0 < |x – a| < δ, entonces |f(x) – L| < ε. Sé que esto puede sonar un poco técnico, pero no te preocupes, lo desglosaremos paso a paso.
Visualizando el Concepto de Límite en un Punto
Una manera útil de entender los límites es visualizándolos. Piensa en una función f(x) y el punto a en el cual queremos encontrar el límite. A medida que nos acercamos a a desde la izquierda y desde la derecha, observamos los valores de f(x). Si esos valores se acercan a L, decimos que el límite en el punto a es L.
Para más detalles sobre cómo visualizar límites, te recomiendo revisar este artículo: Límite Matemático en Wikipedia.
Propiedades de los Límites en un Punto
Los límites tienen algunas propiedades interesantes que los hacen útiles en el análisis matemático. Algunas de las propiedades más importantes son:
1. Linealidad
Si limx→a f(x) = L y limx→a g(x) = M, entonces:
limx→a [f(x) + g(x)] = L + M
2. Producto
Si limx→a f(x) = L y limx→a g(x) = M, entonces:
limx→a [f(x) * g(x)] = L * M
3. Cociente
Si limx→a f(x) = L y limx→a g(x) = M, y M ≠ 0, entonces:
limx→a [f(x) / g(x)] = L / M
Aplicaciones del Límite en un Punto
El concepto de límite en un punto tiene varias aplicaciones prácticas. Aquí te comparto algunas:
1. Continuidad
Una función es continua en un punto si el límite de la función en ese punto es igual al valor de la función en ese punto. Esto es crucial para muchas áreas del análisis matemático y la física.
2. Derivadas
La derivada de una función en un punto se define como el límite de la tasa de cambio promedio de la función a medida que el intervalo se hace infinitesimalmente pequeño. Esto es esencial en el cálculo diferencial.
3. Integrales
Las integrales también se definen usando límites, ya que representan el área bajo una curva, que se aproxima sumando infinitos rectángulos infinitesimalmente delgados.
Desafíos y Trucos para Entender los Límites en un Punto
Entender los límites puede ser desafiante al principio, pero aquí te dejo algunos consejos que me ayudaron en su momento:
1. Practica, Practica y Practica
La mejor manera de entender los límites es resolviendo muchos problemas. La práctica te ayudará a reconocer patrones y a comprender diferentes enfoques.
2. Utiliza Gráficas
Visualizar las funciones y sus límites en gráficas puede ser muy útil. Esto te dará una idea más clara de lo que ocurre cuando te acercas a un punto específico.
3. Estudia Ejemplos Resueltos
Revisar ejemplos resueltos te ayudará a entender el proceso paso a paso. Puedes encontrar muchos ejemplos en línea, como en este recurso: Introducción a los Límites en Khan Academy.
Comparación con Otros Conceptos Matemáticos
Es útil comparar el límite en un punto con otros conceptos matemáticos para entender mejor sus diferencias y similitudes.
1. Límites Laterales
Mientras que un límite en un punto considera la aproximación desde ambos lados, los límites laterales solo consideran la aproximación desde un lado, ya sea desde la izquierda o desde la derecha.
2. Límites Infinitos
Los límites infinitos consideran el comportamiento de una función a medida que se aproxima al infinito. Esto es diferente del límite en un punto, que se enfoca en un valor finito específico.
3. Continuidad
La continuidad de una función en un punto implica que el límite en ese punto existe y es igual al valor de la función en ese punto. Por lo tanto, la continuidad es un concepto relacionado pero más específico.
Recursos Adicionales
Para profundizar en el tema de los límites en un punto, te recomiendo revisar los siguientes recursos:
