La Guía Definitiva
Introducción a Graficar Funciones
¡Hola a todos! Soy Leandro, y hoy quiero compartir con ustedes todo lo que he aprendido sobre cómo graficar funciones. Puede parecer un tema complicado al principio, pero con un poco de práctica y las herramientas adecuadas, se vuelve mucho más sencillo. A lo largo de este artículo, les daré una guía completa, desde los conceptos básicos hasta técnicas avanzadas. ¡Vamos a ello!
¿Qué Significa Graficar Funciones?
Graficar funciones es una habilidad fundamental en matemáticas y ciencias. Básicamente, consiste en representar visualmente una función matemática en un plano cartesiano. Esto permite entender cómo se comporta una función y analizar sus características principales, como máximos, mínimos y puntos de inflexión.
Para aquellos que están comenzando, una función es una relación entre dos conjuntos, donde a cada elemento del primer conjunto le corresponde un único elemento del segundo conjunto. Al graficar, generalmente trabajamos con funciones de la forma y = f(x), donde x es la variable independiente e y es la variable dependiente.
Importancia de Graficar Funciones
Graficar funciones no es solo una tarea académica; tiene aplicaciones prácticas en diversas áreas como la ingeniería, economía, física y más. Al visualizar una función, podemos obtener información valiosa sobre su comportamiento y tendencias, lo que nos ayuda a tomar decisiones informadas.
Por ejemplo, en economía, graficar funciones de oferta y demanda permite entender cómo interactúan estos factores en el mercado. En física, las gráficas de funciones son esenciales para analizar el movimiento de objetos y la relación entre diferentes variables físicas.
Herramientas para Graficar Funciones
Existen múltiples herramientas que facilitan el proceso de graficar funciones. A continuación, mencionaré algunas de las más populares y efectivas:
1. Software de Matemáticas
Programas como MATLAB, Mathematica y GeoGebra son ampliamente utilizados para graficar funciones. Estos programas ofrecen una gran cantidad de funcionalidades avanzadas que permiten crear gráficas precisas y detalladas.
2. Calculadoras Gráficas
Las calculadoras gráficas como la TI-84 y la Casio FX-9750GII son herramientas portátiles muy útiles para graficar funciones. Aunque tienen menos capacidades que el software de matemáticas, son perfectas para uso en el aula y tareas rápidas.
3. Herramientas Online
Existen múltiples plataformas en línea que permiten graficar funciones de manera gratuita. Algunas de las más recomendadas son Desmos, Geogebra y Wolfram Alpha. Estas herramientas son accesibles desde cualquier dispositivo con conexión a Internet y son muy intuitivas de usar.
Pasos para Graficar Funciones
Ahora que conocemos las herramientas, veamos el proceso paso a paso para graficar funciones:
1. Definir la Función
El primer paso es definir la función que deseamos graficar. Asegúrate de tener la expresión matemática correcta y de entender su dominio y rango.
2. Determinar el Dominio y Rango
El dominio de una función es el conjunto de valores de x para los cuales la función está definida. El rango es el conjunto de valores de y que la función puede tomar. Esto es crucial para establecer los límites de la gráfica.
3. Calcular Puntos Clave
Para graficar la función, es útil calcular algunos puntos clave, como los interceptos con los ejes, máximos, mínimos y puntos de inflexión. Esto nos dará una idea más clara de cómo se comporta la función.
4. Trazar la Gráfica
Utiliza la herramienta de tu elección para trazar la gráfica. Asegúrate de etiquetar los ejes y de incluir una leyenda si es necesario.
Ejemplos Prácticos
Veamos algunos ejemplos prácticos de cómo graficar funciones:
Ejemplo 1: Función Lineal
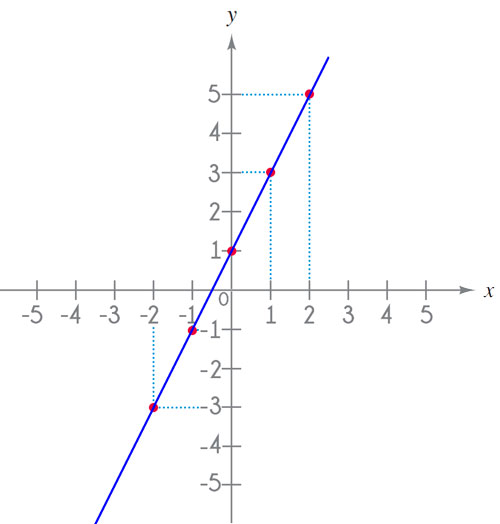
Consideremos la función lineal y = 2x + 3. Esta es una función simple que representa una línea recta. Para graficarla, necesitamos calcular algunos puntos:
- Para x = 0, y = 3
- Para x = 1, y = 5
- Para x = -1, y = 1
Con estos puntos, podemos trazar la línea recta en un plano cartesiano.
Ejemplo 2: Función Cuadrática
Consideremos la función cuadrática y = x^2 – 4x + 4. Esta es una parábola que abre hacia arriba. Calculamos algunos puntos clave:
- Para x = 0, y = 4
- Para x = 2, y = 0 (mínimo)
- Para x = -1, y = 9
Con estos puntos, podemos trazar la parábola en el plano cartesiano.
Consejos y Trucos para Graficar Funciones
Aquí algunos consejos y trucos que he aprendido a lo largo de los años para mejorar la precisión y claridad de las gráficas:
1. Utiliza una Escala Adecuada
Es importante elegir una escala adecuada para los ejes x e y. Una escala incorrecta puede distorsionar la gráfica y hacer que sea difícil de interpretar.
2. Etiqueta y Anota
Asegúrate de etiquetar los ejes y anotar puntos clave en la gráfica. Esto hace que la gráfica sea más fácil de entender y analizar.
3. Verifica con Valores Adicionales
Si no estás seguro de la precisión de tu gráfica, calcula valores adicionales para x y verifica que coincidan con la gráfica.
Recursos Adicionales
Para aquellos que quieren profundizar más en el tema, aquí algunos recursos adicionales:
Conclusión
Graficar funciones es una habilidad esencial que puede facilitar la comprensión de conceptos matemáticos y científicos complejos. Con las herramientas adecuadas y un poco de práctica, cualquiera puede aprender a hacerlo. Espero que esta guía les haya sido útil y que se sientan más seguros al abordar el tema.
¡Nos vemos en la próxima! Soy Leandro, y ha sido un placer compartir este conocimiento con ustedes.
