Todo lo que Necesitas Saber
¡Hola! Soy Leandro, y hoy vamos a hablar sobre un tema que puede sonar un poco técnico al principio, pero que es esencial en el mundo de las matemáticas y las ciencias: las asíntotas. ¿Qué son? ¿Para qué sirven? ¿Cómo influyen en las gráficas de funciones? Te invito a quedarte y descubrir todo esto y más.
¿Qué es una Asíntota?
Para empezar, definamos qué es una asíntota. En términos sencillos, una asíntota es una línea que una función tiende a acercarse a medida que se extiende hacia el infinito, pero nunca llega a tocar. Las asíntotas pueden ser horizontales, verticales u oblicuas, y cada tipo tiene sus propias características y aplicaciones.
Tipos de Asíntotas
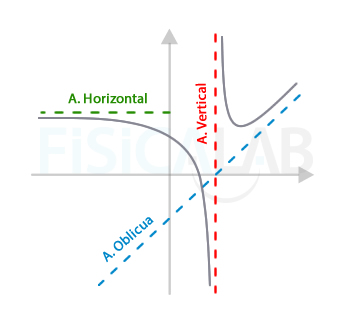
Podemos clasificar las asíntotas en tres tipos principales:
Asíntotas Horizontales
Las asíntotas horizontales son líneas que la gráfica de una función se aproxima cuando la variable independiente se mueve hacia el infinito o menos infinito. En términos prácticos, son útiles para determinar el comportamiento a largo plazo de una función.
Asíntotas Verticales
Las asíntotas verticales son líneas verticales que indican valores de la variable independiente donde la función tiende a infinito o menos infinito. Estas asíntotas son cruciales para identificar los puntos donde la función no está definida.
Asíntotas Oblicuas
Las asíntotas oblicuas son líneas que no son ni horizontales ni verticales, pero que la función se aproxima en su comportamiento a largo plazo. Estas suelen aparecer en funciones racionales donde el grado del numerador es mayor que el del denominador.
¿Cómo Encontrar las Asíntotas de una Función?
Ahora que sabes qué son las asíntotas, el siguiente paso es aprender cómo identificarlas en una función.
Encontrando Asíntotas Horizontales
Para encontrar asíntotas horizontales, debes observar el límite de la función cuando la variable independiente tiende a infinito o menos infinito. Si el límite existe y es un número finito, entonces tienes una asíntota horizontal en ese valor.
Encontrando Asíntotas Verticales
Las asíntotas verticales se encuentran identificando los valores de la variable independiente que hacen que la función no esté definida o tienda a infinito. Esto generalmente implica resolver para los valores que hacen que el denominador de una fracción sea cero.
Encontrando Asíntotas Oblicuas
Para las asíntotas oblicuas, se requiere un análisis más detallado. Generalmente, esto implica dividir el numerador entre el denominador y observar el comportamiento del cociente cuando la variable independiente tiende a infinito.
Importancia de las Asíntotas en Matemáticas y Ciencias
Las asíntotas no son solo un concepto abstracto; tienen aplicaciones prácticas en diversas áreas de las matemáticas y las ciencias. Por ejemplo:
En Física
En la física, las asíntotas se utilizan para modelar comportamientos a largo plazo en sistemas dinámicos. Por ejemplo, la velocidad terminal de un objeto en caída libre puede ser modelada como una asíntota horizontal.
En Economía
En economía, las asíntotas pueden ayudar a modelar comportamientos de mercado a largo plazo, como la tendencia de los precios o el crecimiento poblacional.
En Ingeniería
En ingeniería, las asíntotas son útiles para diseñar sistemas de control y prever el comportamiento de circuitos eléctricos a largo plazo.
Enlaces Relacionados
Para profundizar más en el tema, te recomiendo los siguientes enlaces:
La Competencia en el Nicho de Asíntotas
Al investigar sobre la competencia en este nicho, encontramos que hay varios recursos en línea que abordan el tema de las asíntotas. Sin embargo, muchos de estos recursos son altamente técnicos y pueden ser difíciles de entender para los principiantes. Aquí es donde nuestro enfoque más accesible y desenfadado puede hacer una gran diferencia.
Competencia Destacada
Algunos de los recursos más destacados incluyen:
Conclusión
Espero que este artículo te haya brindado una comprensión clara y completa sobre las asíntotas y su importancia en diversas disciplinas. Si tienes alguna pregunta o comentario, no dudes en dejarlo abajo. ¡Hasta la próxima!
