¿Qué son las Progresiones Geométricas?

¡Hola a todos! Soy Leandro, y hoy quiero llevarlos en un viaje fascinante a través del mundo de las progresiones geométricas. Puede que el término te suene un poco técnico, pero créeme, es una de las herramientas matemáticas más útiles y versátiles que existen.

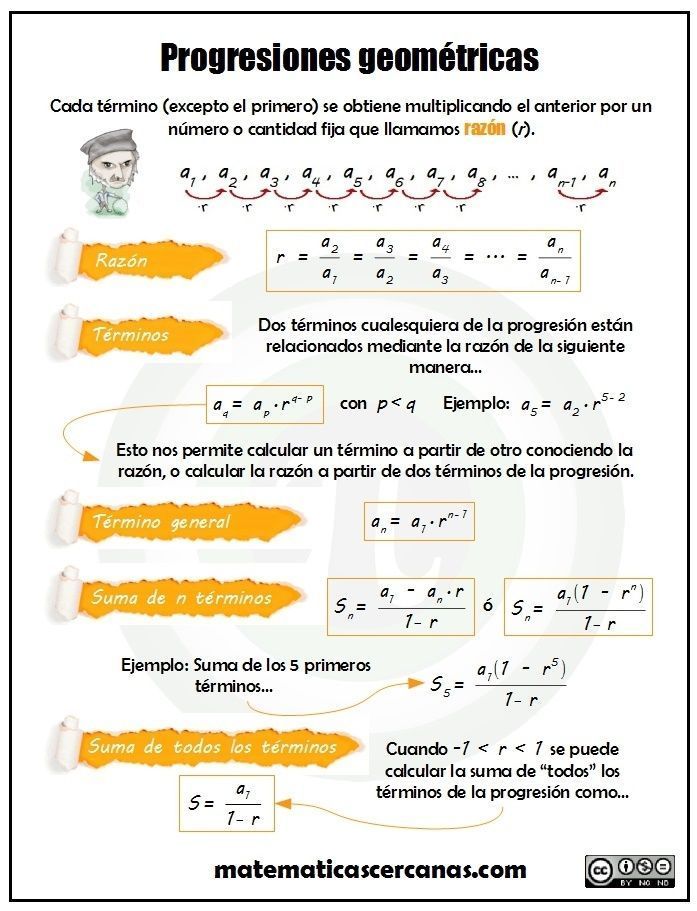
Una progresión geométrica es una secuencia de números donde cada término se obtiene multiplicando el término anterior por una constante llamada «razón». Por ejemplo, en la secuencia 2, 6, 18, 54, cada número se obtiene multiplicando el anterior por 3. Fácil, ¿verdad?

Conceptos Básicos de las Progresiones Geométricas

Para entender bien las progresiones geométricas, es crucial dominar algunos conceptos básicos:

Término Inicial

El término inicial es, como su nombre indica, el primer número de la secuencia. En nuestro ejemplo anterior, el término inicial es 2.

Razón

La razón es el número constante por el cual multiplicamos cada término para obtener el siguiente. En la secuencia 2, 6, 18, 54, la razón es 3.

Fórmula General

La fórmula general de una progresión geométrica es a_n = a₁ * r^n-1, donde a_n es el término enésimo, a₁ es el término inicial, r es la razón y n es la posición del término en la secuencia.

Aplicaciones Prácticas de las Progresiones Geométricas

Las progresiones geométricas no son solo teoría; tienen aplicaciones prácticas en diversos campos. Aquí algunos ejemplos:

Finanzas

En el mundo financiero, las progresiones geométricas se utilizan para calcular intereses compuestos. Si alguna vez te has preguntado cómo crece tu dinero en una cuenta de ahorros, la respuesta está en una progresión geométrica.

Física

En física, estas progresiones se usan para describir fenómenos como el decaimiento radiactivo y la amplificación de señales. Es increíble cómo algo tan simple puede explicar cosas tan complejas.

Informática

Los algoritmos de búsqueda y clasificación en informática también hacen uso de progresiones geométricas. Si eres programador, seguramente te has encontrado con ellas sin darte cuenta.

Cómo Resolver Problemas con Progresiones Geométricas

Resolver problemas con progresiones geométricas puede parecer complicado al principio, pero con un poco de práctica, te volverás un experto. Aquí te dejo algunos pasos para resolver problemas típicos:

Identificar los Parámetros

Lo primero es identificar el término inicial y la razón. Sin estos dos datos, no puedes aplicar la fórmula general.

Aplicar la Fórmula General

Una vez que tienes los parámetros, aplica la fórmula a_n = a₁ * r^n-1 para encontrar el término que necesitas.

Resolver para Diferentes Valores de n

Si el problema te pide encontrar varios términos, simplemente cambia el valor de n en la fórmula y resuelve.

Progresiones Geométricas vs. Aritméticas: ¿Cuál es la Diferencia?

Una pregunta común es la diferencia entre progresiones geométricas y aritméticas. Aunque ambas son secuencias de números, tienen diferencias fundamentales:

Progresiones Aritméticas

En una progresión aritmética, cada término se obtiene sumando una constante al término anterior. Por ejemplo, en la secuencia 2, 5, 8, 11, cada número se obtiene sumando 3 al anterior.

Progresiones Geométricas

Como ya mencionamos, en una progresión geométrica, cada término se obtiene multiplicando una constante al término anterior. La diferencia clave está en la operación: suma para aritméticas y multiplicación para geométricas.

Conclusión

Las progresiones geométricas son una herramienta poderosa y versátil en matemáticas. Desde finanzas hasta física e informática, su aplicación es vasta y variada. Espero que este artículo te haya proporcionado una comprensión más profunda de este fascinante tema. ¡Hasta la próxima!