Conceptos Básicos de Topología
Introducción a la Topología
¡Hola a todos! Soy Leandro y hoy les voy a llevar a un viaje fascinante a través de los conceptos básicos de topología. La topología es una rama de las matemáticas que puede parecer un poco abstracta al principio, pero una vez que te sumerges en ella, te das cuenta de lo omnipresente y útil que puede llegar a ser.
¿Qué es la Topología?
En términos simples, la topología estudia las propiedades de los espacios que se mantienen a través de deformaciones continuas como estiramientos, torsiones y contracciones, pero no desgarros ni pegados. En otras palabras, la topología se centra en las propiedades que no cambian cuando un objeto es transformado de manera continua.
Historia y Origen de la Topología
La topología surgió a principios del siglo XX y ha evolucionado desde entonces. Fue inicialmente conocida como «geometría de posiciones» y ha crecido para abarcar una vasta cantidad de subcampos y aplicaciones. Algunos de los pioneros en este campo incluyen a Leonhard Euler y Henri Poincaré.
Conceptos Fundamentales de la Topología
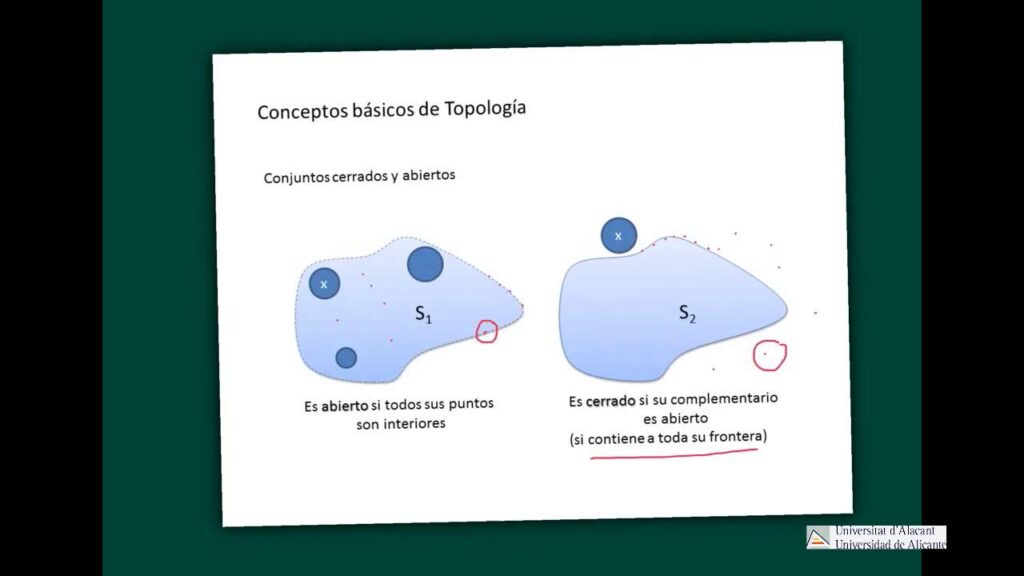
Conjuntos Abiertos y Cerrados
Uno de los conceptos básicos de topología es la idea de conjuntos abiertos y cerrados. En un espacio topológico, un conjunto abierto es, en términos simples, un conjunto que no incluye sus fronteras. Por otro lado, un conjunto cerrado incluye sus fronteras. Estos conceptos son fundamentales para definir otros términos topológicos.
Espacios Topológicos
Un espacio topológico es un conjunto de puntos, junto con una familia de conjuntos abiertos que cumple ciertas propiedades. Estas propiedades son:
- El conjunto vacío y el conjunto total son abiertos.
- La intersección de un número finito de conjuntos abiertos es abierta.
- La unión de cualquier colección de conjuntos abiertos es abierta.
Homeomorfismos
Un homeomorfismo es una función continua entre dos espacios topológicos que tiene una función inversa también continua. En esencia, si dos espacios son homeomorfos, son topológicamente equivalentes. Esto significa que pueden ser transformados uno en el otro mediante deformaciones continuas.
Subespacios Topológicos
Un subespacio de un espacio topológico es cualquier subconjunto de ese espacio con la topología inducida. La topología inducida se define de tal manera que un conjunto es abierto en el subespacio si y solo si es la intersección del subconjunto con un conjunto abierto del espacio más grande.
Aplicaciones de la Topología
La topología tiene aplicaciones en diversas áreas de la ciencia y la ingeniería. A continuación, se presentan algunas de las aplicaciones más destacadas:
Topología y Física
En física, la topología se utiliza para estudiar propiedades como la continuidad y la conectividad en sistemas físicos. Un ejemplo famoso es la teoría de las cuerdas, que utiliza conceptos topológicos para describir las propiedades fundamentales del universo.
Topología y Biología
En biología, la topología se aplica en el estudio de estructuras como el ADN y las proteínas. Por ejemplo, se utiliza para entender cómo las proteínas se pliegan y cómo las moléculas de ADN se enredan y desenredan.
Topología y Computación
En ciencias de la computación, la topología se usa en áreas como la teoría de grafos y el análisis de algoritmos. Los conceptos topológicos ayudan a diseñar y analizar redes y estructuras de datos complejas.
Recursos Adicionales
Si deseas profundizar más en los conceptos básicos de topología, te recomiendo los siguientes recursos:
Conclusión
Espero que esta introducción a los conceptos básicos de topología te haya resultado interesante y útil. La topología es una rama de las matemáticas que, aunque puede parecer abstracta, tiene aplicaciones prácticas en muchas disciplinas. Si te interesa saber más, te animo a explorar algunos de los recursos adicionales que he mencionado. ¡Hasta la próxima!
