Introducción a la estimación de pi a través de simulaciones
¡Hola! Soy Leandro, y hoy vamos a sumergirnos en el fascinante mundo de la «Estimación de pi a través de simulaciones». Si alguna vez te has preguntado cómo se puede calcular el valor de pi sin recurrir a fórmulas matemáticas complejas, estás en el lugar adecuado. Vamos a explorar juntos distintos métodos, sus ventajas y desventajas, y cómo puedes implementarlos tú mismo. ¡Vamos allá!
¿Qué es pi y por qué es importante?
Antes de adentrarnos en las técnicas de estimación, es crucial entender qué es pi (π). Pi es una constante matemática que representa la relación entre la circunferencia de un círculo y su diámetro. Es un número irracional, lo que significa que no puede ser expresado como una fracción exacta y su representación decimal es infinita y no periódica. Pi es fundamental en diversas áreas de la matemática y la física, y su valor aproximado es 3.14159.
Métodos comunes para la estimación de pi
Existen múltiples métodos para estimar el valor de pi, desde los más tradicionales hasta los más innovadores. Aquí vamos a centrarnos en aquellos basados en simulaciones, que son especialmente interesantes por su aplicabilidad y facilidad de implementación con un poco de programación.
Método de Monte Carlo
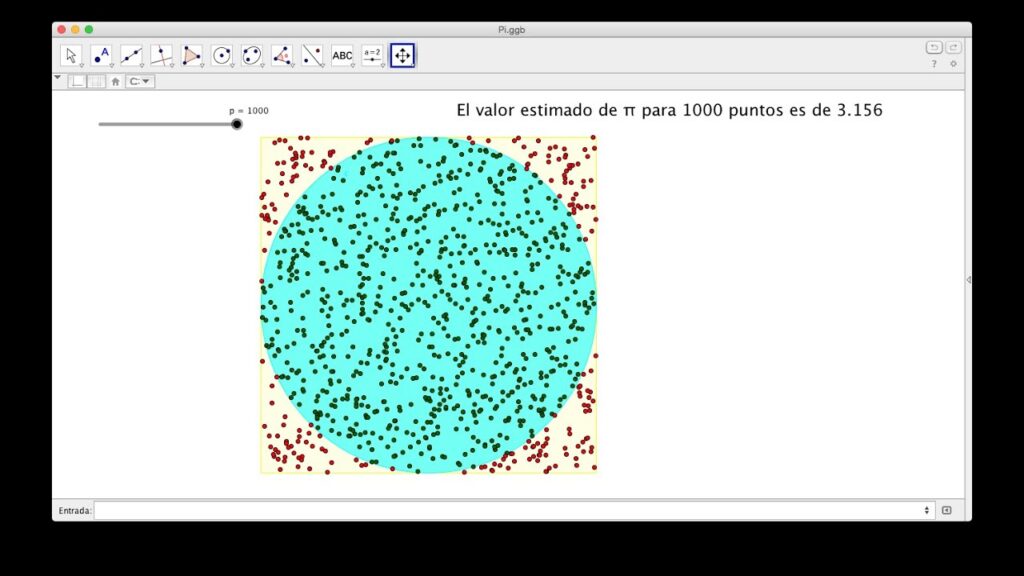
El método de Monte Carlo es quizás uno de los más conocidos y utilizados para la estimación de pi. La idea básica es simular un gran número de puntos aleatorios en un cuadrado de lado 2 y contar cuántos de esos puntos caen dentro de un círculo inscrito en el cuadrado. La relación entre el número de puntos dentro del círculo y el total de puntos generados se puede utilizar para aproximar el valor de pi.
La fórmula es simple: Pi ≈ 4 * (número de puntos dentro del círculo / número total de puntos). Este método, aunque sencillo, requiere una gran cantidad de puntos para obtener una estimación precisa.
Método de Buffon
El método de Buffon es otro enfoque interesante para estimar pi. Este método se basa en un experimento de probabilidad que involucra lanzar agujas sobre una superficie con líneas paralelas separadas por una distancia igual a la longitud de la aguja. La probabilidad de que una aguja cruce una de las líneas está relacionada con el valor de pi.
La fórmula para estimar pi en este caso es: Pi ≈ (2 * longitud de la aguja * número de lanzamientos) / (número de cruces de líneas). Aunque este método es menos intuitivo que el de Monte Carlo, ofrece una perspectiva única sobre cómo la geometría y la probabilidad pueden combinarse para estimar constantes matemáticas.
Simulación de series infinitas
Las series infinitas también pueden utilizarse para aproximar pi. Un ejemplo es la serie de Leibniz, que es una serie infinita alternante que converge a pi/4. La fórmula es la siguiente: Pi/4 ≈ 1 – 1/3 + 1/5 – 1/7 + 1/9 – …
Para implementar esta fórmula, simplemente sumamos un gran número de términos de la serie. Este método es fácil de entender y programar, pero como la serie converge muy lentamente, se necesitan muchos términos para obtener una estimación precisa.
Implementación de simulaciones para estimar pi
A continuación, vamos a ver cómo podemos implementar estas simulaciones utilizando un lenguaje de programación como Python. No te preocupes si no eres un experto en programación; los ejemplos serán sencillos y fáciles de seguir.
Implementación del Método de Monte Carlo
Vamos a empezar con el método de Monte Carlo. Aquí tienes un ejemplo de código en Python:
import random def estimar_pi(num_puntos): dentro_circulo = 0 for _ in range(num_puntos): x = random.uniform(-1, 1) y = random.uniform(-1, 1) if x**2 + y**2 <= 1: dentro_circulo += 1 return 4 * dentro_circulo / num_puntos num_puntos = 1000000 pi_estimado = estimar_pi(num_puntos) print(f"Estimación de pi: {pi_estimado}")Este código genera un millón de puntos aleatorios y estima el valor de pi utilizando el método de Monte Carlo. Puedes ajustar el número de puntos para ver cómo afecta la precisión de la estimación.
Implementación del Método de Buffon
Ahora vamos a ver cómo implementar el método de Buffon:
import random import math def estimar_pi(num_lanzamientos, longitud_agujas, distancia_lineas): cruces_lineas = 0 for _ in range(num_lanzamientos): x = random.uniform(0, distancia_lineas / 2) angulo = random.uniform(0, math.pi) if x <= (longitud_agujas / 2) * math.sin(angulo): cruces_lineas += 1 return (2 * longitud_agujas * num_lanzamientos) / (cruces_lineas * distancia_lineas) num_lanzamientos = 1000000 longitud_agujas = 1 distancia_lineas = 1 pi_estimado = estimar_pi(num_lanzamientos, longitud_agujas, distancia_lineas) print(f"Estimación de pi: {pi_estimado}")En este ejemplo, lanzamos un millón de agujas y estimamos el valor de pi utilizando el método de Buffon. Como en el caso anterior, puedes ajustar el número de lanzamientos para ver cómo cambia la precisión.
Implementación de la serie de Leibniz
Finalmente, vamos a implementar la serie de Leibniz para estimar pi:
def estimar_pi(num_terminos): suma = 0 for i in range(num_terminos): termino = (-1)**i / (2*i + 1) suma += termino return 4 * suma num_terminos = 1000000 pi_estimado = estimar_pi(num_terminos) print(f"Estimación de pi: {pi_estimado}")Este código suma un millón de términos de la serie de Leibniz para estimar el valor de pi. Nuevamente, puedes ajustar el número de términos para ver cómo afecta la precisión de la estimación.
Comparación de métodos para la estimación de pi
Ahora que hemos implementado varios métodos, es importante comparar sus ventajas y desventajas. Aquí tienes una tabla resumen:
| Método | Ventajas | Desventajas |
|---|---|---|
| Método de Monte Carlo | Fácil de entender e implementar | Requiere muchos puntos para una estimación precisa |
| Método de Buffon | Interesante desde el punto de vista probabilístico | Menos intuitivo y requiere muchas simulaciones |
| Serie de Leibniz | Fácil de programar | Convergencia lenta |
Competencia en el nicho de la estimación de pi
La estimación de pi es un tema ampliamente discutido en la comunidad matemática y de programación. Algunos de los recursos más populares incluyen:
Estos recursos ofrecen una visión en profundidad de los métodos y teorías detrás de la estimación de pi.
Conclusión
La «Estimación de pi a través de simulaciones» no solo es una manera efectiva de calcular esta constante matemática, sino que también es una excelente oportunidad para aprender sobre programación, probabilidad y geometría. Espero que este artículo te haya proporcionado una comprensión clara y práctica de los diferentes métodos disponibles y cómo puedes implementarlos. Si tienes alguna pregunta o comentario, no dudes en dejarlo abajo. ¡Hasta la próxima!
