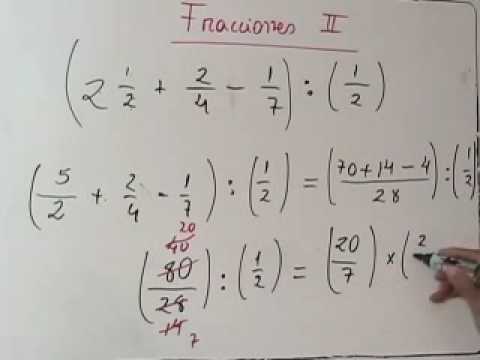
Todo lo que necesitas saber
Introducción a las Fracciones II
Hola, soy Leandro y hoy vamos a sumergirnos en el apasionante mundo de las fracciones. Pero no te preocupes, no estamos hablando de fracciones básicas. Este artículo, titulado «Fracciones II», está diseñado para llevarte más allá de los conceptos básicos y explorar aspectos más avanzados de las fracciones. Así que, prepárate para una clase magistral informal pero extremadamente detallada.
¿Qué son las Fracciones II y por qué son importantes?
Las fracciones II no son más que el siguiente nivel en el estudio de fracciones. Mientras que en las fracciones básicas aprendemos a identificar, sumar, restar, multiplicar y dividir fracciones simples, en las Fracciones II nos adentramos en temas más complejos como fracciones compuestas, fracciones algebraicas y su aplicación en problemas más avanzados.
Fracciones Compuestas
Definición y Ejemplos
Las fracciones compuestas son aquellas fracciones en las que tanto el numerador como el denominador son fracciones a su vez. Por ejemplo, la fracción (3/4) / (5/6) es una fracción compuesta. Para resolver este tipo de fracciones, se suele utilizar la multiplicación cruzada.
Cómo resolver fracciones compuestas
Para resolver una fracción compuesta, se multiplica el numerador por el recíproco del denominador. Utilizando nuestro ejemplo anterior, (3/4) / (5/6) se resolvería como (3/4) * (6/5). El resultado sería 18/20, que se puede simplificar a 9/10.
Fracciones Algebraicas
¿Qué son las fracciones algebraicas?
Las fracciones algebraicas son fracciones en las que el numerador y/o el denominador son expresiones algebraicas. Por ejemplo, (x+2)/(x-3) es una fracción algebraica. Este tipo de fracciones se utilizan mucho en álgebra y cálculo.
Resolviendo fracciones algebraicas
Para resolver fracciones algebraicas, se siguen los mismos principios que para las fracciones numéricas, pero añadiendo un paso extra: la simplificación de las expresiones algebraicas. Por ejemplo, si tenemos (x^2 – 4)/(x^2 – 9), podemos factorizar ambos términos para obtener ((x+2)(x-2))/((x+3)(x-3)).
Aplicaciones de las Fracciones II en la vida real
Las fracciones avanzadas tienen múltiples aplicaciones en la vida real, desde la ingeniería hasta la economía. Por ejemplo, en ingeniería, las fracciones se utilizan para calcular tensiones y fuerzas en estructuras. En economía, se utilizan para calcular tasas de interés y ratios financieros.
Recursos adicionales para aprender sobre Fracciones II
Para aquellos que quieran profundizar aún más en el estudio de las fracciones, aquí hay algunos recursos útiles:
